Lesson κ': Book I, Proposition 47

This is the most famous geometrical theorem, known by those who know no other geometry

That the square on the hypotenuse equals the squares on the legs of a right triangle was known in ancient cultures world-wide, as well as the familiar 3,4,5 triangle and other right triangles with integer sides. It was not discovered by Pythagoras, though it carries his name to honour him, and was not first proved by Euclid. Euclid's proof is not the most obvious, or the one that would be chosen if only this result were required. Indeed, many proofs are known, and a book has been filled with them. What was new with Euclid was that the proof was rigorously shown to be a consequence of the Postulates, and that many consequences are drawn from it that were unknown and unsuspected elsewhere. Although it crowns Book I, we appreciate that it is not an advanced result of Greek mathematics, but a rather humble one. It is included here because of its popular fame.

Euclid delays his proof of this theorem until after the theory of parallels has been worked out. Then, the theorem is elegantly shown to be a nearly obvious consequence of this theory. A lot of water has passed under the bridge since Proposition 5. The properties of triangles have been worked out, as well as the relations of parallel lines and the angles they make with lines crossing them. We now can draw parallels, construct squares, and do other useful things. We know that the areas of parallelograms depend only on their base and height, and that a triangle with the same base and between the same parallels as a parallelogram has half its area. After all this, Euclid throws out the proof of the Pythagorean theorem as a simple application.

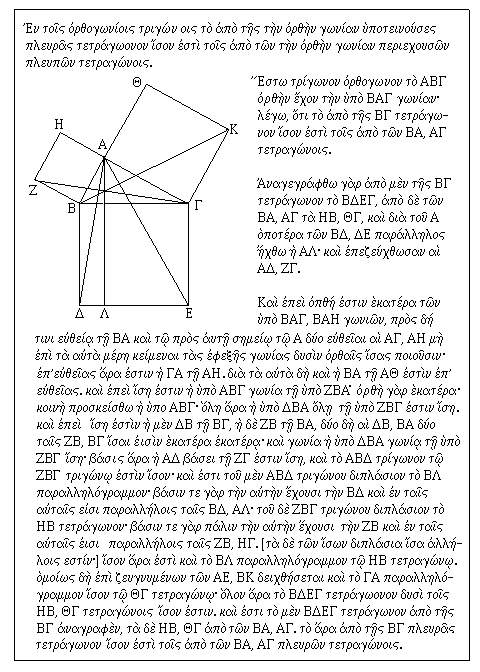The text is given at the right. Nearly all the words used will be already familiar to you if you have been following the course. The less-familiar words have been picked out and are listed in a vocabulary box below. That the list is so short shows that the same words are used over and over in Euclid, and this is what makes it easy to read. The statement of the theorem is, rather literally: "In right triangles the square on the side subtending the right angle is equal to the squares on the sides enclosing the right angle." Note that the word order is totally different, but the Greek gets all the modifiers in front of the noun to make the meaning clear. The application to the figure is: "Let there be a right triangle ABΓ having a right angle BAΓ I say, that the square on BΓ is equal to the squares on BA, AΓ."

As usual, we think about the problem before tackling the proof, and try to establish a method of procedure. If we can show that square HB is equal to the rectangle BΛ, and the square AK is equal to the rectangle ΛΓ, we will have a proof. Now, the rectangle BΛ is twice the triangle ABΔ (same base, between same parallels), while the square HB is twice the triangle ZBΓ for the same reason. If we can show that the two triangles are equal, then we have what we want. The triangles have two sides equal, each to each, because squares have equal sides. The obtuse angles are each a right angle plus the same angle, angle ABΓ, so the triangles are equal by SAS. We can do the same for the square AK. Well, that is the proof, so let us proceed.

The construction now follows. Only the part necessary for the first half of the proof is done now, since it is simply duplicated for the second half, and we need only refer to this then. "Let square BΔEΓ be described on BΓ, and HB, ΘΓ on BA, AΓ, and through A to each of BΔ, ΔE parallel let AΛ be drawn; and join AΔ, ZΓ." We have already used these lines in devising a method of proof. Incidentally, this shows the great power of the diagram. It is not mere decoration, but a valuable tool.

Here is the vocabulary. The adjective orqogwnios I suspect has the same endings for masculine and feminine; we only find it modifying a neuter nound. u(potei/nwn is a present active participle of the most common type. The hypotenuse "subtends" the right angle. The word for square may be familiar, but it is worth noticing that it does not refer to any figure with four angles. a)nagra/fw here means to write upon, specifically referring to the sides on which the squares are to be drawn. proskei~mai is a deponent, meaning that it has middle endings for an active meaning. "To lie" is quite obviously middle, since the subject is what does the lying. It is only an active verb in English. the third-person present middle endings are -tai and -ontai.

Well, then, let's finally get started. "And since both BAΓ, BAH are right angles, at some straight line BA and at the point A, two straight lines AΓ and AH not lying towards the same parts the successive angles make two straight angles; in a straight line, therefore, is ΓA to AH. Through the same indeed also BA is to AΘ in a straight line." Here is something we did not think of above. From the figure, it was obvious that AH and AΓ were in the same straight line. It is not good enough that it be obvious, however; it must be proved, since we did not get HA by extending AΓ.

"And since angle ΔBΓ is equal to ZBA, each [is] a right angle; let the common ABΓ be added; the whole, therefore, ΔBA is equal to the whole ZBΓ. And since on one hand ΔB is equal to BΓ and on the other ZB to BA, the two ΔB, BA are indeed equal to ZB, BΓ, each to each; Also angle ΔBA is equal to angle ZBΓ; Therefore, the base AΔ is equal to the base ZΓ, and the triangle AB&Delta is equal to the triangle ZBΓ" We have established that the two triangles are equal at this point, and are about to apply the relations between the areas of triangles and parallelograms with the same base and altitude.

"And the BΛ parallelogram is double the triangle ABΔ; having the same base and in the same parallels BΔ, AΛ; The square HB is double the triangle ZBΓ likewise having the same base ZB and in the same parallels ZB, HΓ. [those that are doubles of equals are equal to each other;] Therefore, the parallelogram BΛ is equal to the square HB. Similarly, joining AE, BK, it will be shown that the parallelogram ΓA is equal to the square ΘΓ; The whole square BΔEΓ is therefore equal to the two squares HB, ΘΓ. And the square BΔEΓ is described upon BΓ, HB, ΘΓ on BA, AΓ. Therefore, the square on the side BΓ is equal to the squares on the sides BA, AΓ." The proof is complete, just as we planned it. The text in square brackets is an interpolation not in the original text. It is, of course, superfluous, and is typical of later specious additions.

The concluding paragraph is shown on the right, and you should be able to read it without assistance. It is exactly like the statement of the theorem, with the addition of a/)ra, therefore, and the omission of gwni/an, which a later commentator has supplied.

Composed by J. B. Calvert
Created
Last revised 16 June 2002