Lesson κε': A Theorem From The Phaenomena

The Phaenomena is an astronomical book also attributed to Euclid, but probably the work of Autolycus of Pitane (315-240 BC)

In addition to the Elements, the name of Euclid is also attached to a number of other mathematical works, among which is the Phaenomena, the faino/mena, or appearances, which describes the diurnal motion of the fixed stars and the ecliptic, the path of the planets. It is an elementary work, intended to familiarize the student with celestial motions. The presentation is partly a narrative, partly formal propositions, but is much less rigorous than the Elements. The figures seem mainly to be sketches showing relative positions, usually based on the circle of the horizon, and not constructed to true scale or shape. The actual constructions are contained in more advanced works, such as those by Autolycus, and involve multi-view drawings. The origin and correctness of the figures seem somewhat doubtful, and the figures do indeed differ between the two recensions that are the basis of all surviving texts. It is, however, worth reading for the vocabulary and the insight into how the universe was regarded. The results of the Phaenomena were of most use to astrologers, of course. However, the Phaenomena is a purely scientific treatise, and contains no hint of superstition.

The view of the universe in the Phaenomena is the majority one that survived until the 17th century and the age of Kepler and Galileo. It is based purely on appearances, in which the earth is stationary at the centre of the universe, towards which all weight tends. The stars are located on a fixed sphere, all at the same enormous, but still comfortable, distance beyond the sun, moon and planets. The reason given for this conclusion is that the relative positions of the stars do not change when one moves about on the earth. This implies that either the stars are all at the same distance, or that they are at a gigantic, overwhelming, inconceivable distance. Common sense preferred the more likely explanation. The first proposition of the Phaenomena is that the earth is at the centre of the rotating sphere of the stars, and is proved by observation, that stars on exactly opposite parts of the firmament are seen directly opposite each other from the earth. The earth, of course, is very much smaller than the firmament, but the whole universe is comfortably and comprehensibly enclosed in a sphere of reasonable size. This apparent universe is the one that our senses tells us actually exists. Not one person in a thousand today could tell you any way to discover that the facts are completely different, and the words and concepts of religion still preserve the old views, and speak of the universe in exactly the same way.

Whatever one believes about the structure of the heavens, for practical purposes the celestial sphere is still the most convenient mode of description, and is used today. The real motions make no change whatsoever.

One of the two fundamental astronomical motions is the daily rotation of the earth, which is mirrored in the apparent rotation of the sky from west to east once in each sidereal day, in which a star on the meridian at its start returns to the meridian again. The Phaenomena deals with this motion, as perceived by an observer on the surface of the earth. To get a feel for the Phaenomena, let us study one of the shorter propositions, Proposition 3, which states: "Any fixed star, which rises and sets, always rises and sets at the same point of the horizon." This is proved simply by establishing that the star describes a small circle about the axis of the firmament, and the plane of this circle cuts the horizon circle at two points, those of rising and setting. The figure for the proposition simply shows a few circles that suggest the facts, unlike the Elements, when the figures are rigorously constructed.

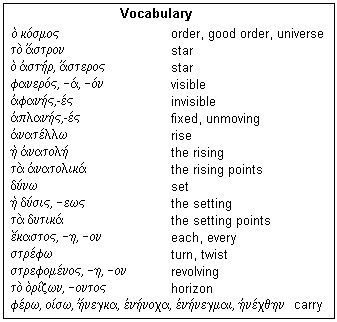Since we are dealing with a new subject, astronomy, we will find a different vocabulary. The words needed for Proposition III are listed in the box at the left. The word ko/smos comes from the verb kosme/w, "order" or "arrange." It has received the figurative meaning of "universe" or even "mankind" as expressing the ordered reality of experience. There are two common words for star, one masculine and one neuter; the neuter is used in the Proposition. Both words include what we call the planets, from pla/nhs, "wanderer," but not the sun and moon. The stars proper are the fixed stars, and the adjective uses the α-privative. Stars may be visible, when above the horizon, and invisible, when below. Because of the diurnal motion, stars rise and set, and here are the words for these phenomena. Anatolia was the land of the rising sun, the East with respect to Constantinople. The horizon is the "cutting" or "division", from the verb o(ri/zw, "divide" and ideally seen in the line dividing sea and sky. The middle and passive of the verb stre/fw is used for "revolving" as in the motion of the celestial sphere; we find the participle in the Proposition. To strengthen this sense, we may use the middle of the verb fe/rw, which curiously has the same sound as the Latin fero, which means the same thing. All six principal parts of this verb are given, since this is one of the terrible examples of irregular stem formation (as it is in Latin). Several different verbs have been conflated here into a single verb. As a review, the principal parts are: present, future, aorist, perfect, perfect middle, aorist passive, in the first person singular, and give all the stem forms used to conjugate the verb.

Now to the proposition. "Of the fixed stars making their risings and settings, each rises and sets at the same points of the horizon. In the cosmos, let ABΓ be the horizon, and the circle AΔE the largest of the always visible circles, the [circle] BHZ largest of the always invisible [circles], and choose the star Θ of those making risings and settings, and let the risings be in the parts Γ, and the settings in the parts K; I say, that the point Θ always rises and sets at the same points of the horizon while the sphere revolves." Note the genitive absolute. Now the demonstration follows: "Let KΘΓ be the circle on which Θ is carried; Therefore, the circle KΘΓ cuts the horizon and is perpendicular to the axis of the sphere. All circles perpendicular to the axis and cutting the horizon make the risings and settings at the same points of the horizon. Therefore, the circle KΘΓ always rises at the point Γ, and always sets at the point K. Furthermore, the star Θ is carried on the circumference of the circle KΘΓ; and therefore the star Θ always rises at the point Γ, [and] sets at the point K."

As you can see, the proposition merely emphasizes that the fixed stars move on circles perpendicular to the axis, and so share the properties of these circles. The determination of the points of rising and setting is not attempted in this Proposition, since it is a more difficult matter requiring special analysis. Let us, therefore, look at how these points can be found.

A graphical solution of the problem of the points of rising and setting of a fixed star, as well as the times of rising and setting, is shown in the Figure below. This is a modern multi-view orthographic projection, but similar methods were used in antiquity for solving the same problem. Autolycus α' is given in the scholia to the Phaenomena as the source of the solution. In the present case, the upper view is the one shown in the Phaenomena, the circle representing the horizon, as was usually done. The view below is an elevation, with the observer at O and the plane of the horizon represented by the line NS. The circle is the observer's meridian. The celestial pole is in the direction of P. The auxiliary view at an angle looks directly down the axis from P towards O, and the circle is the diurnal circle of the star B. The elevation view shows the declination δ of the star, and the elevation of the pole, which is the observer's latitude φ. The diurnal circle of the star is represented by a line in this view, which represents a plane intersecting the horizon at the points of rising and setting. The diameter of the diurnal circle is found by projection from the elevation view. It is not really necessary for the solution, but shows the path of the star across the sky during the rotation of the celestial sphere, which is clockwise in this view. The three points A, D and B determine a circle, which must be the one drawn in the figure of Proposition III. However, this circle is simply a way to locate the points, and does not actually represent a projection of the diurnal circle of the star.

It greatly aids understanding to make your own drawing. The first thing is to draw the circles representing the horizon and meridian in the same positions as shown in the Figure. Now draw the line OP at the angle of the latitude, the equator CG perpendicular to it, and lay off the angle δ that is the declination of your chosen star. It is good to do this for a star you know, and for your actual latitude. Now draw BA through B parallel to the equator. From its intersection A with the horizon, draw a line perpendicularly upward crossing the horizon in the plan view, and determining the points of rising, A, and of setting, D. This solves the problem, and the angles of A and D from North can be read off using a protractor. With a level horizon, this is where your star will rise and set. If you know the right ascension of your star, and the sidereal time on the day (which locates the vernal equinox), it is easy to find the times of rising and setting as well.

Composed by J. B. Calvert
Created 23 August 2000
Last revised 16 June 2002