The Pleasures of Mathematics

The greatest pleasures of mathematics and science are in understanding. Here is an example.

Much too often science and mathematics are presented as Gee Whiz, or as the ability to perform calculations, or to answer Jeopardy-style questions, or even to feel superior to those of lesser knowledge. The enjoyment of these things soon palls and becomes stale. The real fascination is in understanding the world, not just describing it. As one example, consider the five Platonic solids, the convex regular polyhedra. Why are there just five, no more and no less? It is easy to reason why this is the case, but most of the people who are acquainted with the solids and display them to their pupils have no idea. Reasoning is quite a great distance away from our schools, though it is given lip service.

If you have not thought about proving that there are only five regular convex polyhedra, read on and see if you do not think it is satisfying to know how. A regular polyhedron has faces that are regular polygons, connected at their edges. All the polygons must be the same size, since they meet evenly at their edges. The ends of the edges are the vertices of the polyhedron. At each vertex, a certain number of edges lead away, making the same angles with each other. In a convex polyhedron, the edges are all on one side of a plane containing the vertex. The polygons must each have at least three sides, and at least three edges must meet at a vertex, or we will not have a polyhedron. Now suppose the polygons have N sides, and that M edges meet at a vertex. Both N and M must be three or greater.

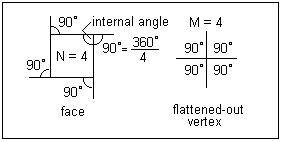Consider a vertex, which will resemble the top of a pyramid of M sides. Imagine it squashed flat, as in the figure on the right. This action will make each of the angles between the edges somewhat larger, but the resulting angle cannot be any larger than 360°/M. This gives us a maximum angle between the edges of the polygons that comprise the faces. If we now look at the polygons, we can determine these angles from the number of sides N. Extending each side a little, we find N equal external angles that add up to 360°:, so that each is 360°/N. The internal angle is 180° less this angle, or 180° - 360°/N. In the Figure, both these angles happen to be 90°, since N = 4. We have just found that this angle cannot exceed 360°/M. This gives us the following inequality:

180° - 360°/N < 360°/M

Dividing by 180°, we find 1 - 2/N < 2/M, or NM - 2M -2N < 0. Adding 4 to each side, NM - 2M - 2N + 4 < 4. Factoring this, we find (N - 2)(M - 2) < 4, the condition that must be satisfied by any M, N. We see at once that neither M nor N can exceed 5, so the only possible values are 3, 4, and 5. The following table exhausts all the possibilities:

M	N	Figure
5	3	Icosahedron
3	5	Dodecahedron
4	3	Octahedron
3	4	Cube
3	3	Tetrahedron

The faces of the polyhedron can be only triangles, squares and pentagons. If we try M = 4 and N = 4, we see that four squares can meet at a vertex only if they lie in a plane, and so do not make a polyhedron. Of course, here (4 - 2)(4 - 2) = 2 × 2 = 4, which is not less than 4. M = 3 and N = 6 lead to a similar conclusion. In each case, we have a tesselation of the plane, but no polyhedron. Now it is quite clear why there are only five regular solids, and we know it not because someone has said so, but through our knowledge of space.

That there are only five regular polyhedra has been known for more than 2500 years, but the fact is much less important than the reasoning used to establish it. This method was unique to the classical world of Greece and Rome, and has led to modern science and understanding. It is, unfortunately, still the possession of only a few people, and is sadly lacking in modern mass education.

The illustration at the link to this page is an anaglyph of a dodecahedron. View it through red-green 3-D glasses to see the polyhedron in space.

Composed by J. B. Calvert
Created 9 December 2000
Last revised