Filters

Twin-T Notch, Sallen and Key Lowpass, and Multiple Feedback Bandpass

Filters in General

There are numerous examples of filters in the other units, especially the ubiquitous RC low- and high-pass filters that we considered in the unit on the time and frequency domains. A filter is a linear system whose frequency response H(ω) is its important property, used to modify a signal by the frequency domain rule X(ω) = H(ω)Y(ω) for a linear system. It is generally described in the frequency domain, but it must be remembered that this implies certain time domain properties as well, which may be important. For example, if waveform is to be preserved, its various frequency components must all have the same delay in the filter. Also, square waves may exhibit overshoot, undershoot or ringing quite prominently after going through a filter. In fact, looking at the square wave response is a good way to test a filter.

H(ω) is described by plotting the magnitude in dB or the phase shift in degrees or radians against the logarithm of the frequency. The resulting Bode plots are familiar to electronics engineers, and are much more useful than linear plots, as we found in the case of RC circuits. A decade of frequency is a factor of 10, as from 1kHz to 10kHz. Gain in dB is given by 20 log (V_out/V_in), so a ratio of 1/2 is -6 dB. The 20 is so that dB expresses the power ratio in the same resistance, and is conventional.

The gain and phase shift as a function of frequency can have any form, with very general relations between them. Nevertheless, certain common forms of frequent use have been given descriptive names. The meanings of lowpass, highpass, bandpass and band rejection or notch filters should be obvious. There is nothing implied about the detailed shape of the response, only the general nature. A lowpass filter has a pass band to indefinitely low frequencies, where the gain may vary somewhat, or even vary linearly, and have bumps and sags. It has a stop band where the gain is very low, often decreasing continously as the frequency increases, called rolloff. The two bands are separated by a knee, and the frequency of the knee is often called the corner frequency. These parameters only have precise meanings when defined with relation to a specific form of the response curve. The corner frequency is very often defined operationally as the frequency at which the magnitude of the gain is 1/√2 = 0.707, or -3 dB.

Passive filters are made up only of linear circuit elements R, L and C. Inductance is found usually only in filters for high frequencies, where it is easy to supply without great size or weight. Resistance and capacitance make up most passive filters for lower frequencies. One exception used to be the ripple filters on power supplies, which used iron-core inductors, for good filtering without excessive capacitance, which was expensive at high voltages. An example of a passive filter is, of course, an RC circuit, which is a first-order filter, meaning that the response rolls off as 1/f, or 20 dB/decade. The order of a filter can be estimated from the number of reactive elements it contains. An LC combination, for example, gives a second-order filter. The reactive elements must play the principal role in the filtering, of course, not just be around. Loading is always a problem with passive filters, either with respect to the source and load, or to different parts of the same filter. One can cascade RC branches for added filtering, but the attenuation is soon quite large.

The problem of loading is solved in active filters by including an amplifier. Active filters can be very effective, even when quite simple, and are not difficult to design and construct. Let's now look at some practical examples of passive and active filters.

Twin-T Notch Filter

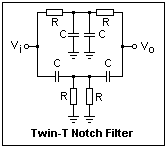Sometimes a filter to remove a certain frequency band is required. If this is a narrow band, the filter is called a notch filter. A notch filter using only resistors and capacitors is shown at the left. It is really two filters in parallel, the upper one lowpass and the lower one highpass, with the stop bands overlapping. The reason it is called "twin-T" should be obvious. It's a good example of a passive filter. The frequency of minimum gain is f_o = 1 / 2πRC. For R = 10k and C = 0.01 μF, f_o = 1591 Hz. To block 60 Hz, R = 2.7k and C = 1 μF will be close to correct.

The largest problem with this filter is that the input resistance is low at high frequencies, being approximately R/4. As with all passive filters, the source and load affect its properties, unless the filter is buffered. I tested a filter with R = 10k and C = 0.01 μF, and found the gain at f_o to be around -42 dB, with a bad waveform. This is not bad for a passive notch filter of such simple design. The high frequency gain was down because of the 600Ω output impedance of the function generator working into the high frequency resistance of about 2.5K.

Estimate the bandwidth of the filter by adjusting the frequency until the gain is 0.707 at the high and low points. This gives the frequencies f_L and f_H for the -3 dB points. The Q of the filter is f_o/(f_H - f_L), the center frequency divided by the bandwidth. This is only exactly true for certain response curves, but is good figure of merit. For my filter, I found f_H = 6485 Hz, f_L = 377 Hz, so Q = 0.26, a rather low figure. Usually, one wants a much higher Q, but this circuit has its uses.

Sallen and Key Lowpass Filter

An excellent and useful example of an active filter is shown at the right, in the form of a second-order lowpass filter, a type very often required. By interchanging resistors and capacitors, it becomes a highpass filter with similar characteristics. The op-amp is used as a buffer, holding the node at the inverting input at the output voltage V_o. There is positive feedback in this circuit, but it never overcomes the negative feedback, so the circuit is stable.

Circuit analysis, using 1/jωC for the impedance of a capacitor, gives V = V_o + jωCV_oR = V_o(1 + jωCR). In the same way, V_i = V + [jωCV_o + jωC(V - V_o)] = V(1 + jωCR). Therefore, V_o/V_i = 1 / (1 + jωCR)². This response is second-order because it contains the square of the frequency in the denominator. At high enough frequencies, the gain will vary as f^-2, or 40 dB per decade, twice the slope of a simple RC filter. The frequency f_o = 1/2πRC is called the pole frequency. The tangent of the phase angle is -2(f/f_o) / (1 - (f/f_o)²). Therefore, the phase angle will lead by 90° when f = f_o, and by 180° at high frequencies, twice the phase shift of a first-order circuit.

Construct a filter with R = 10k and C = 0.01 μF, which should give a pole frequency of about 1591 Hz. Use any op-amp, such as the 411, and a bipolar supply so the input and output can swing around ground. At this frequency, the voltage gain, which is simply 1 / (1 + f/f_o)² is 0.5, or -6 dB. Measure the gain of the filter at frequencies from 100 Hz to 10 kHz, and plot dB against log f. Observe that the rolloff is at 40 dB/decade, and that the -6 dB point is near 1590 Hz. The phase difference between the output and input can also be measure. The Lissajous figure gives an ellipse with vertical and horizontal axes at this frequency, which means 90° phase shift.

Multiple Feedback Bandpass Filter

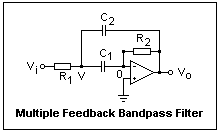We should look at a bandpass filter, so we can find out the significance of Q, and design a filter with a reasonable value of it. A suitable circuit is shown at the right. Feedback is taken from the output to two points in the input network. There is only one node of unknown voltage, so the solution is easy. Any current in C₁ comes from the output via R₂, and is, in fact, just V_o/R₂. This has to go through the impedance of C₁, so V = -V_o/jwC₁R₂. The current thorugh C₂ is (V_o - V)jωC₂. These two currents unite to flow through R₁, and this gives us V_i in terms of V_o. This kind of analysis is not hard, and a little practice will develop considerable skill with it.

The next step is to solve for V_o/V_i = -jωC₁R₂ / [1 - ω²C₁C₂R₁R₂ + jωR₁(C₁ + C₂)]. This is a general expression for the gain. Now we let C₁ = C₂ = C for simplicity, define k to be √(R₂/R₁), and f_o = 1 / 2πC√(R₁R₂). A little simplification gives - jkff_o / [f_o² - f² + 2jff_o/k] for the gain. At this point we make an approximation. When f is near f_o, the gain curve is almost symmetrical, and we now make an approximation that renders it exactly symmetrical, and gives us a simple expression. If we don't do this, things remain complicated and obscure in the algebra. Let Δf = f_o - f, and then the difference of squares becomes 2f_oΔf, and everywhere else we put f = f_o.

We now get V_o/V_i = - j(k²/2) / [j + kΔf/f_o]. This shows us that if we take Q = k/2, then f_o/Q will be the width between the -3 dB points, as it is usually defined. Then, V_o/V_i = -2jQ² / [j + 2QΔf/f_o]. This is the simple expression that gives the response near the maximum. To find the amplitude response, multiply this expression by its complex conjugate and take the square root. We find |V_o/V_i| = 2Q²/[1 + (2QΔf/f_o)^1/2. Similarly, the phase is given by tan φ = 2QΔf/f_o. This is quite a long route, but a detailed map has been given to enable you to follow it.

We now know the Q and f_o in terms of the resistance and capacitance values, and the form of the response. The maximum gain of 2Q² occurs at f_o, and the -3 dB points are a distance f_o/2Q on either side of the maximum. The phase changes from 45° at the lower -3 dB point, f_L to -45° at the upper -3 dB point, f_H. If you ask what happens on the skirts of the response, the answer must be taken from the original full expression, not the approximation we use near the maximum. It is seen that the response falls to zero on either side, ultimately at -20 dB/decade, and the phase angle is 0° at low frequency, and 180° at high frequency. As for any second-order filter, the total rolloff is -40 dB/decade (here half on each side), and the total phase change is 180°.

I made a filter with Q = 1.9 and f_o = 411 Hz by taking C = 0.01 μF, R₁ = 10k, and R₂ = 150k, and using a 411 op-amp with ±12 V supplies (to allow for the gain of about 8 at the maximum). If you do this, find f_o by changing the frequency until the output on the scope is a maximum. Then find f_H and f_L the same way, looking for 0.707 of the maximum. Finally, measure the gain at a few points on each skirt, from 10 Hz to 10kHz, so you can estimate the slopes. I measured f_o = 400 Hz and Q = 1.9, which are very close to the calculated values. It is very instructive to plot the response curve and see what it looks like. It is much sharper than the minimum for the twin-T notch filter, because of the larger value of Q.

References

Filter design is a very well-developed, large and complex field. Horowitz and Hill give excellent practical information and advice on designing active filters for various uses in Chapter 5. There is also Don Lancaster's Active Filter Cookbook (Indianapolis, IN: Howard Sams, 1975, 1985) with a large amount of well-presented information. As usual, it isn't a "cookbook" but rather a careful treatment of the fundamentals, directed towards understanding.

Composed by J. B. Calvert
Created 28 July 2001
Last revised