We have treated RC filters, and active filters using op-amps, on other pages. Now let's consider LC filters, which are widely used at radio frequencies because practical inductors are easily made, even with air cores. The field of passive LC filters is a large and well-developed one. Here, we only want to cover the basics, and investigate how certain simple filters behave in the laboratory.
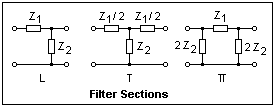The diagram at the right shows three simple filter sections, L, T and Π, constructed symmetrically with impedances Z1 and Z2. The sections shown are essentially the same; which is chosen depends on the particular use. More than one filter section may be cascaded to obtain a higher-order filter.
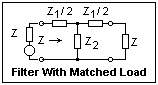At radio frequencies, we often want to match impedances to eliminate reflections (when the size of the apparatus is comparable with the wavelength) or to maximize power transfer. The diagram at the left shows a generator with internal impedance Z feeding a matched load of impedance Z through a T-section filter. We want the impedance "looking into the filter" to be Z as well in the band of operation. Easy circuit analysis shows us that this impedance Z = √(Z1Z2 + Z12/4). It should be clear that Z will always vary with frequency if the impedances are reactive, which is the only interesting case. Filters made only of resistors are merely attenuators, and not very exciting. The filters we are considering will be made of inductors and capacitors.
If we restrict ourselves to the case Z1Z2 = k2, where k is real, and has the dimensions of a resistance, we will call the resulting filters constant-k filters. Then, Z = k√(1 + Z1/4Z2). The simplest filters result when Z1 = jωL and Z2 = 1/jωC, or vice-versa. If L is the series element, we have a lowpass filter, and if C is the series element, a highpass filter. These are the only two kinds of filters that result from this choice. In what follows, we shall replace k by R, to remind us that we are dealing with a resistance. Then, for the lowpass filter, R2 = L/C (the frequency having cancelled, as it must if k is to be a constant). The quantity Z1/4Z2 = -(πf)2LC = -(f/fo)2, where fo = 1/π√(LC) is the cutoff frequency. Now, Z = R√[1 - (f/fo)2], which shows us that for frequencies much below the cutoff frequency, the impedance looking into the filter is indeed R. This result is approximate, not exact.
Let us now consider such a filter, with a constant resistance R as a load. We can calculate the transfer function as in the case of an RC filter, and obtain Vout/Vin = 1 / [(1 - ω2LC) + jωL/R]. The absolute value of this expression decreases as f-2 for f >> fo, or -40 dB/decade, as is typical of a second-order filter. There are two reactive elements, L and C, so we do indeed have a second order filter. When f = fo, the gain is 0.2774 or about -11 dB. Note that fo is not the usual corner frequency at which the gain is 3 dB down. The properties of a highpass circuit can be worked out in the same way, and equivalent results obtained. The LC filter, being second order, is a bit more practical than the single-section RC filter. Now let's look at LC filters in the laboratory.
It is convenient to work with 3.3 mH inductances and 0.01 μF poly capacitors. The 3.3 mH inductances are typical radio-frequency chokes (RFC), and just about any value you may happen to have in this area can be used. The function generator has an internal impedance of 600 ohms, so I chose R = 600Ω, and used a 620Ω resistor as a load. There is nothing sacred about this resistance value, which has no effect in the experiments we are about to do. In a practical RF case, you may well be working with sources, loads or transmission lines of a certain impedance, and there it may be important. Check your values by connecting an inductor and capacitor in parallel, with a 620Ω load, and finding the resonant frequency, which should be about 28 kHz for the values given.
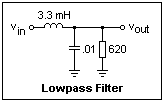Perhaps a lowpass section is a good place to start. The circuit is shown at the right. Look at the input and output voltages with the oscilloscope, using a sinusoid from a function generator as the input. Count the frequency for reasonable accuracy; function generator dials are not very accurate. Find the gain over at least a decade in frequency. In this case, the cutoff frequency is about 55 kHz, but nothing special will be happening at it, except that the gain will be falling off at 40 dB/decade. Take about 10 points, and plot gain in dB against log f. Note where -11 dB comes, and check that it occurs at about the cutoff frequency calculated from the component values. What is R?
Repeat your measurements for a highpass filter, simply interchanging L and C.
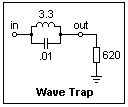The inductor and capacitor can be connected as a parallel resonant circuit, and used in a wave trap, as shown in the figure on the left. This is not a constant-k filter, but it is again a second-order filter. At the resonant frequency, it gave an attenuation of -21 dB into the 620Ω load, which is not bad. As you know, at parallel resonance, the circuit is resistive, presenting a resistance of Q2R, where R is the effective resistance of the inductor (not the R that is equal to k!). In this case, the resistance was about 6400Ω. This is an example of a notch filter, used for removing an unwanted signal.
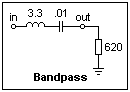If a series resonant circuit is used instead, we have a bandpass filter. For the filter shown at the right, the response rolls off at about 20 dB/decade on either side of the center of the passband (28 kHz). This is not a very exciting rolloff for a bandpass filter, since sharper edges are usually desired. Be sure that you look at the action of the notch and bandpass filters; it is instructive to observe them.
If we want better notch and bandpass filters, we have to go to higher orders. Suppose that Z1 = jωL + 1/jωC, for the inductor and capacitor in series. If R = √(L/C) as before, then Z2 = 1/ (jωC + 1/jωL), which is the same inductor and capacitor, but now in parallel. This yields two constant-k fourth-order filters, one a notch filter, and the other bandpass, which are shown below.
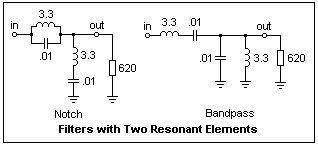
The notch filter gave an attenuation of -27 dB in the notch, while the bandpass filter showed rolloff of -40 dB/decade on either side of the passband, which is more satisfactory behavior. Build these circuits and test them. Note that it is simple to decide what type of filter you have by inspection, in all the cases we have studied, considering either the limits of high and low frequencies, or parallel or series resonance.
If you want a fourth-order lowpass filter, simply cascade two LC sections. Since the impedance looking into the filter is the same as the load, the two sections work the same way, each seeing the same load. My filter apparently overperformed, giving -108 dB/decade where it should have been only -80. At any rate, the rolloff is impressively rapid. The gain was down 3 dB at 32 kHz, and already down about 21 dB at 64 kHz.
Composed by J. B. Calvert
Created 31 August 2001
Last revised