The Eccles-Jordan Circuit and Multivibrators

Astable, monostable and bistable circuits, Schmitt triggers and multivibrators, using tubes, transistors and integrated circuits.

Although both the IEEE Standard Dictionary of Electrical and Electronic Terms and the Cambridge Dictionary of Science and Technology have entries for "Eccles-Jordan," the name has vanished from most modern texts on electronics and digital design, though the circuit it describes is the fundamental circuit of computers, now known as the "flip-flop." Any state machine, and a computer is simply a huge state machine, can be built from Eccles-Jordan circuits and logic gates. The circuit was discovered in 1919 [Radio Review, 1, 143] as a development of the multivibrator, described the year before by H. Abraham and E. Bloch in Publication 27 of the French Ministère de la Guerre, and in Annales de Physique 12, 252 (1919). [These men are not the more famous M. Abraham and L. Bloch.] This was in the early days of the three-element amplifying thermionic lampe-valve, before there was any application for a "memory" circuit. Before discussing the Eccles-Jordan circuit, it is appropriate to study the multivibrator from which it was derived.

The circuit of the Abraham-Bloch multivibrateur, so-called because its output is rich in harmonics, is shown at the right. It is also called a plate-coupled multivibrator. The tube shown is a dual triode with common cathode, but a tube with independent cathodes, or two separate tubes could be used. Each triode forms an inverting amplifier capacitor-coupled to the other. The overall gain is -1 x -1 = +1, so the circuit is unstable and will oscillate. Instead of a sinusoidal oscillation at some high frequency, relaxation oscillations will result, since the gain is unity at all frequencies down to zero. The circuit is called an astable, since neither of its internal states persists indefinitely. The wave form depends on the ratio R₁/R₂, its amplitude on R₁, and its frequency on the values of C and R₂ (mainly). The plate current is the current that results for zero grid bias with the given plate supply voltage.

When the circuit is first turned on, imagine that both tubes are conducting equally, and nodes "c" and "d" are at some low voltage, with a small charge on C and the grids at ground potential. If the right-hand triode happens to conduct slightly less, then node "d" rises in voltage, and the rise is immediately conducted to the grid of the left-hand triode. This triode then conducts even more heavily, so node "c" drops in voltage. Again, this is communicated to the grid of the right-hand triode, which consequently conducts even less. This is an unstable situation, and the right-hand triode is soon cut off, so that node "c" rises towards V_bb, charging the left-hand capacitor C to a considerable voltage.

Now the left-hand triode is conducting heavily, while the right-hand triode is cut off. Let's call this State 1. The right-hand capacitor C soon charges, allowing the grid of the right-hand triode to approach ground. As soon as this triode conducts, node "d" falls in voltage. The left-hand C is fully charged, so this fall is communicated to the grid, and node "c" rises, reinforcing the positive swing of the grid on the right-hand triode. Node "d" soon sinks near ground, taking the left-hand grid to a large negative voltage. At this point, the left-hand triode is cut off, while the right-hand triode is conducting heavily. We call this State 2.

Now the left-hand capacitor C discharges through its R₂. Eventually, the grid approaches ground and conduction begins again. As before, the condition is unstable because of the interaction of the two triodes, and soon State 2 has become State 1 again. The other capacitor C makes the other grid very negative, and again the charge on this C leaks off to ground. The two capacitors C take turn in charging when their plate nodes go high, and discharging when their plate nodes go low. Do not be frustrated if the action is not clear to you at this point; it is remarkably difficult to keep things straight. Experiment is a great help in this--simply probe any point with the scope to discover how it behaves.

A practical multivibrator circuit is shown at the right. The 6N7 dual triode is probably not ideal for this service, but I chose it because it is a rugged tube, and I expected to make mistakes. The 6SN7 or 12AU7 dual triodes were classically used for multivibrators, and they would work well here as well. This circuit, in which R₁ << R₂, gives the characteristic square-wave output at the plates, with a sharp negative spike at the leading edge of the negative phase. When, on the other hand, R₁ >> R₂, the waveform at the plates is a series of decreasing and increasing exponential ramps of large amplitude.

Study the plate waveforms using different values of R₁ and R₂. Note that the amplitude of the main plate swing (ignoring the negative spike) is proportional to R₁, which can have values between 4.7k and 47k (10k seems a good value). R₂ can be anything between 10k and 1M, and has the principal effect on the period of oscillation. Also look at the grid waveforms, which are a series of exponential decays (tube off) and constant values near zero (tube on).

A transistor realization of the Abraham-Bloch circuit is shown at the left. It is almost exactly the same as the vacuum-tube circuit, except for one detail. If the base resistors were returned to ground, the circuit would not oscillate, since both transistors would be cut off. Unlike a vacuum tube, a transistor does not conduct with zero base-emitter voltage. When the bases are raised to the point of conduction, as shown, oscillation begins immediately. If the collector resistors are too small, the transistors will not saturate, and the circuit will not oscillate. The collector waveform is a square wave with a slow leading rise, and a sharp drop, with the full amplitude of 0 to 12 V. The bases are driven negative on each transition. In fact, this drive is large enough to worry about the base-emitter junction breakdown, though no problem was experienced here. The frequency was about 19 kHz with the component values shown. The collector waveform switched between 0 and 12 V, with a slow rising edge but a sharp trailing edge. There have been many circuit refinements to improve the waveform and other factors, but here we are only interested in seeing how it works.

The circuit at the right is a multivibrator of the type invented by O. E. Schmitt [Jour. Sci. Instr., 15, 24-26 (1938)], also called a cathode-coupled multivibrator. The coupling to the right-hand triode is through a capacitor, as in the Abraham-Bloch circuit, except that the grid is pulled up to E_bb through a large resistance, so that this triode is normally on. Coupling to the left-hand triode is through the cathode resistor. The normal plate current of about 5 mA puts the cathodes at about 50 V. The grid of the left-hand triode is held at a voltage depending on the adjustment of the 50k pot. Initially, adjust this pot to maximum. When the grid bias is sufficiently high, both tubes conduct, and this is an unstable state. If the right-hand triode conducts a little less, the voltage across the cathode resistor decreases, causing the left-hand tube to conduct more, and the plate voltage drops, which drives the grid of the right-hand tube more negative. This produces State 2, where the left-hand tube is conducting and the right-hand tube is cut off.

Now the capacitor discharges, and the grid of the right-hand tube becomes more positive, eventually causing this tube to begin to conduct. This raises the cathode potential, so the left-hand tube conducts less. This cooperative process continues until the left-hand triode is cut off, and the right-hand triode is conducting, its grid pulled high as the voltage at the plate of the other triode increases. This is State 1. The capacitor now charges as the grid draws a little current, and eventually the drop in cathode current turns on the left-hand triode, whose grid has remained at a fixed potential.

The waveform at the output, the plate of the right-hand triode, is shown at the right. It is much closer to a square wave than in the case of the Abraham and Bloch circuit, but there is still a negative overshoot. The circuit is now "free wheeling" or running at its natural frequency. It is possible to synchronize the oscillations with an external sine wave by applying the external sine wave at the grid of the left-hand triode, coupled through a capacitor. If you do this (not using the differentiating RC circuit), trigger the scope on the signal from the signal generator and observe both the synchronizing and output signals. The frequency can be varied over a considerable range around 2 kHz, and the multivibrator will be phase locked to the synchronizing signal. Synchronization can also be obtained at multiples of the multivibrator's natural frequency, as well as with a string of pulses instead of a sine wave. Note the phase relations as the frequency of the synchronizing signal is varied. It is like a phase-locked loop in effect, but the operation is quite different.

If you reduce the bias at the grid of the left-hand tube, eventually it will be negative enough to keep the tube cut off. I found that oscillation ceased when this voltage was about 43 V. The adjustment is somewhat sensitive. When the left-hand tube is cut off, the circuit remains in State 1, with the right-hand triode conducting and V_o = 150 V (200 V less 5 mA x 10k). The only function of the 10k plate resistor is to produce the output swing. If, however, the grid of the left-hand tube is momentarily positive enough to cause the tube to conduct, the resulting instability causes the circut to pass to State 2. From State 2, it automatically returns to State 1 after a time that depends on the component values.

The 0.01 capacitor and 1k resistor are a differentiating circuit to produce a series of alternating positive and negative pulses from a square wave. A 9 V trigger amplitude is sufficient to produce rectangular pulses at the plate of the right-hand triode. The width of the pulses can be adjusted somewhat by the 2.5M potentiometer. The frequency of the trigger pulses can be varied over a wide range, while the length of the output pulses remains constant. Such a circuit, with one stable state and one unstable state, is called a monostable or single-shot. The original nickname for the circuit was flip-flop, but in about 1950 this term was appropriated by the bistable circuit. The term sometimes heard as a Kipp circuit is not a name, but is derived from the German kippen, to tilt or fall.

Waveforms for the triggered monostable are shown at the left. The grid bias was set at 43.5 V. A square wave from the signal generator was connected to the RC differentiating circuit to produce trigger pulses as shown in the figure. A peak of 9 V appeared to give reliable triggering. Note that the negative-going pulse is ineffective, since it only makes a cutoff bias even greater. The trigger frequency can be varied over a very wide range while the pulses remain the same length, which is roughly the same as for the astable case. Triggering is essentially different than synchronization. It is asynchronous, an output pulse occurring whenever the trigger pulse arrives. The trigger is not active during the output pulse, so this monostable is not retriggerable.

Another single-shot is shown at the right. The tube used is the 14AF7 loktal dual medium-mu triode. The more expensive 7AF7, the 6SN7, or any similar dual triode can be used. In the normal state, V₂ should be on (the grid-cathode potential near zero), and the voltage developed across the 4.7k cathode resistor should be sufficient to cut off V₁. In this circuit, the plate current of a bit over 3 mA makes this voltage 15V. Therefore, the plate of V₁ is near 120V, and the timing capacitor C is charged. Originally, I tried a cathode resistor of 2.0k, and this was not enough to cut off V₁. The plate resistor for V₁ must be large enough to saturate the plate when V₁ is triggered on. This pulls the grid of V₂ well below cutoff, and gives the rising edge of the output pulse.

The circuit was triggered by the positive pulses produced by differentiating a square wave from the signal generator, as above. The pulses must be high enough to overcome the bias on V₁. With the values shown, the output pulse width was 150 μs. The pulse width is approximately 1.5RC. The output pulse amplitude was 65V, with a rise time on the order of 1 μs. The wave form was the same as shown in the figure above, with an undershoot of 10V at the trailing edge. There was about a 400 ns delay from the leading edge of the trigger pulse to the leading edge of the output pulse. The pulse width was independent of the repetition rate, as it should be.

The monostable circuit can be modified into a bistable circuit by removing the capacitor, and feeding the grid of the right-hand triode by a voltage divider. The present circuit uses transistors instead of vacuum tubes. The voltages are lower, and the resistors of accordingly lower values, but the similarity is obvious. V_in should be connected to a low-impedance variable voltage source so the base bias can be easily altered. When V_in is low (less than 2 V), Q1 is certainly cut off, so Q2 is conducting (the collector current is about 2 mA) and the emitter voltage is about 2 V. When V_in is high (less than 3 V), the voltage at node "c" has dropped sufficiently that Q2 is cut off. These are the two stable states of the circuit, corresponding to output voltages of about 2 and 12 V.

If you build the circuit, and watch node "b" while increasing V_i, you will note that it rises with the input voltage at the same time that node "c" is falling, and the resulting "scissors" effect makes the transition rapid. If then you decrease V_in, Q1 continues to conduct until the voltage at node "b" stops following the input, and the opposite transition occurs. The output transition from low to high occurs for an input voltage of 2 V, and the transition from high to low for an input voltage of 3 V. There is, in this case, about 1 V of hysteresis. This circuit is well known as a Schmitt trigger

This analysis also shows us that the circuit has two stable states when V_i is biased to between 2 and 3 volts. In this range, positive and negative triggers will cause transitions between the stable states. This is similar to the behavior of the astable circuit, which became monostable over a certain range of bias. You might want to see if you can cause the bistable circuit to toggle by triggering it with pulses of opposite sign, such as the differentiating circuit produces.

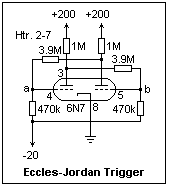Finally we are ready to discuss the important circuit mentioned at the top of this page, the Eccles-Jordan, shown at the left. In it, the capacitors of the Abraham-Bloch multivibrator are replaced by resistors. These resistors pull up the grids of the triodes until both conduct, and this state of unstable equilibrium collapses into State 1 or State 2, depending on which triode remains conducting. Both states are persistent, and do not decay into each other. The grid resistors must be returned to a negative voltage of about -20 V for proper operation of the circuit. In this state, a negative pulse applied to the grid of the triode that is conducting causes a transition to occur. You can simulate such a pulse by touching a wire connected to ground to the proper grid momentarily. Like all mechanical contacts, this will bounce, but multiple pulses have the same effect as one. They are, in effect, "debounced" in this circuit, which is a set-reset flip-flop in modern terminology.

A transistor Eccles-Jordan circuit is shown at the right. Again, it is just like the multivibrator, except that the capacitors have been replaced by resistors. Since the bases are now conductively tied to the collector supply, it is not necessary to bias the transistors "on." A negative pulse at the base of the "on" transistor will cause a transition, as will a positive pulse at the base of the "off" transistor. Use a wire in series with a 1k resistor to simulate the pulses (do not connect a base directly to +12 V!). The 100Ω resistors are not necessary for operation, but help to make the circuit more symmetrical by swamping differences in the transistors.

In digital logic, the two triodes or transistors are represented by logic inverters. The output of one inverter is connected to the input of the other. NAND gates give both the necessary inversion, as well as inputs for the set and reset functions. It is possible to make astable and monostable circuits in this way as well. In fact CMOS logic gates make excellent square-wave oscillators, as is studied in another page. Monostables also are found as integrated circuits, which are easy to use and inexpensive.

The 74LS122 is a Retriggerable Monostable Multivibrator, or "single-shot," that can be used to make pulses of a wide range of widths. The 74LS123 has two such single-shots in a single package. Complementary outputs Q and /Q are provided, so positive and negative pulses are easily available. The circuit is triggered on the high-to-low transition of the trigger input, upon which Q goes low and /Q goes high. The pulse width, t_w, is controlled by an RC time constant: t_w = 0.45 RC, approximately. The 74LS122 contains an internal 11k resistance that can be used for R, or an external resistor between 5k and 180k can be used. The timing capacitor C is best when 1 nF or greater (so stray capacitances do not have a large effect), and is chosen for the range of pulse widths desired. For C = .001 (1 nF) the pulse width using the built-in resistance is about 4 μs; for C = .01, 40 μs; for C = 0.1, 0.4 ms, and so on. A 50k or 100k rheostat in addition to the internal resistance allows the period to be increased up to a factor of 5 to 10 in each case, so the whole range 4 μs - 4 ms is covered with capacitors from .001 to 1.0 μF. The circuit works quite well and stably in this range.

The internal arrangement of the LS122 is shown at the left. To trigger, either A1 or A2 must go low, B1 and B2 must both be high, and CLR must not be activated. This permits many variations of trigger inputs. The CLR immediately terminates the output pulse when it is pulled low, and inhibits further triggering. If the single-shot is triggered during a pulse, the pulse is lengthened for its full amount beyond the trigger. If the circuit is continuously retriggered before the end of the pulse, the output remains low constantly. This feature can be used as a "watchdog," for as long as retriggering pulses arrive quickly enough, the output remains low. A high output (timed out) will show that triggers have not arrived as expected. The diagram also shows the connections for the timing R and C. The C pin is connected internally to ground, but it is best to ground it externally as well. R/C can be connected to +5 through an external timing resistor if desired, or the R pin can be connected directly to +5 to use the internal timing resistor (11k).

Bistable circuits were originally known as triggers (a term now restricted to the pulses, or to the Schmitt trigger), and became known inelegantly as flip-flops when used in computers after about 1950, as has been mentioned. They exhibit the quality of "memory" since their states are maintained as long as the power is applied. Other devices, such as magnetic cores (direction of magnetization) and capacitors (charged or not) also exhibit memory, and can be miniaturized to a much greater extent than discrete tubes and transistors. The capacitors forming dynamic memory are the smallest memory devices so far, and only need to be refreshed every couple of milliseconds, which is a long time in computer life. Still, the Eccles-Jordan bistable and its progeny are still found everywhere and are basic to computer operation. We have merely touched a vast field of knowledge about circuits of this type, but may have explained their principles of operation to some degree.

Composed by J. B. Calvert
Created 22 November 2001
Last revised 30 July 2002