Color
The availability of suitable LED's suggests experimentation with color mixing
Excellent LED's of colors ranging over the visible spectrum have recently become available, prompting this page on color and color mixing. Originally, we had only red LED's, and not very bright ones. Then orange was offered, yellow, and a rather yellowish green. Finally, a few years ago, we got some rather bright LED's, displaying an intense spot inside a clear encapsulation, and finally blue LED's and even white ones, all of which seemed to be bright. A white LED has a continuous spectrum from 450-650 nm. A bright green InGaN LED caught my attention, because of its wavelength, 525 nm, a pure green, and its intensity of 10 cd. With these new LED's it is possible to carry out some excellent color-mixing demonstrations.
First, though, it will be informative to review some ideas on color and illumination, and find out what is meant by an intensity of 10 candela. The human eye is sensitive to radiation between about 400 and 700 nm, the sensitivity peaking at 555 nm and falling off quickly at longer and shorter wavelengths. We actually have two visual systems, the older scotopic system mediated by the rod cells in the retina, and the newer photopic system mediated by the cone cells. We are not usually aware of the scotopic system, since at normal light intensities the rods are bleached out and return no information. It comes into play, however, in the dark-adapted eye, and gives us a very sensitive system for dark nights. A half-hour or so is required for it to become active, and most people are not aware of it at all. I mention it here because the only sensation is one of intensity, shades of gray, without color. It is not very good for seeing details, but is very sensitive to motion in all parts of the visual field, so it can warn of danger very effectively.
The photopic system, on the other hand, presents a world of color. Originally, there were two kinds of cone cell, with slightly different photosensitive proteins or pigments modified from those in the rods. One protein was more sensitive to blue (short wavelengths), the other to yellow (long wavelengths). The difference between the responses of these cells is interpreted by the mind as color, which helps greatly to distinguish different objects in the field of vision that may be of the same brightness (a common situation). This is actually a rather rich variety of sensation, and I think all animals with cone vision possess it (as well as the scotopic gray scale). Some animals, including most people, have split the yellow cones into two varieties with slightly different photosensitive proteins. The difference in response between them gives a scale of color from green to red. Some authorities say that this might have helped to distinguish food from leaves, with evolutionary advantage. It also helps distinguish red from green traffic lights, also an evolutionary advantage.
A few people, mainly men, have not fully differentiated the two types of yellow cones. If there is no differentiation, these individuals are said to have red-green color blindness. The term "color blindness" is a bad one, since there is no blindness involved at all, merely a difference in color perception. Such people are not aware of any sensory lack, except the difficulty of this distinction. There are other variations in color perception, even rarer than this, and the variations can all be traced to irregularities in the photosensitive proteins. The color sensation we describe here is the one common to most people.
Normal color vision, then, is based on three retinal proteins and is called trichromatic. Thomas Young and J. C. Maxwell elaborated the trichromatic theory of color vision purely on the basis of experiment in the early 1800's, since even the structure of the retina was not known then. When the structure of the retina was finally elucidated, the rods and the cones were found, but all the cones seemed exactly alike (as indeed, structurally, they are). Alternative theories to trichromaticity were proposed (notably one by Edwin Land, who was color-blind!). However, the three different proteins have now been isolated, and their spectral absorptions measured, so the trichromatic theory is supported by anatomy. This has had no significant effect on the theory of color, which was always empirically based and successful. There is much more on the eyes and color vision elsewhere on this website, under Optics and Visual Perception.
Brightness is the fundamental subjective visual sensation. Curiously, we can even say when two fields of different color are equally bright (using special apparatus), or that one is brighter than the other. Other than this, we can't put numbers to brightness, or say that one object is twice as bright as another. This is typical of sensations, like the loudness of a sound or the hotness of water. It is possible, however, to adjust the physical intensities, in W/cm2, of two nearly monochromatic light sources of different wavelengths so that they appear equally bright. In this way, we can determine the relative effectiveness of different wavelengths at producing brightness. If we know the spectral power density of a certain light signal, we can multiply the energy in each small wavelength interval by its relative effectiveness and add them up, obtaining a number we can use to compare the brightness of light sources. Theoretically, this number is the integral of the product of the spectral density p(λ) times the effectiveness y(λ), or Y = ∫p(λ)y(λ)dλ. To give this number a definite value related to the physical power of the light, a unit of luminous flux called the lumen (lm) is defined so that at 555 nm, 680 lm = 1 W.
The lumen is a very curious quantity, half in the physical world, half in the subjective. It can only be used to compare two lights as less than, equal to, or greater than. 2 lm is twice as much flux as 1 lm, corresponding to twice the physical power if the spectrum is the same, but it is not twice as bright. Illumination is defined as luminous flux per unit area. The lm/m2 is called the lux (lx) or metre-candle, while the lm/ft2 is the foot-candle (ft-cd). An illumination of 50 ft-cd is ample for drafting and fine work (such as at your lab bench), while you can read a paper at 10 ft-cd, and average room illumination is somewhat less than this level. These specifications are higher than were once common, when 5 ft-cd was thought adequate for ordinary reading and writing.
Suppose you are sitting at a desk with a reading lamp supplying 50 ft-cd, in an average room, and then you turn off the lamp. The brightness is less, obviously, perhaps half or a third as bright as when the desk lamp was on. But if you measure the illumination, you may find it only 3-5 ft-cd, a tenth or even smaller than it was before. This shows that the impression of brightness varies much more slowly than illumination. In fact, the variation is approximately logarithmic, another characteristic of sensation. Our visual system adapts readily to sunlight at thousands of ft-cd and to a room at a few ft-cd. It could not do this if the response were linear.
If an isotropic point source of light emits Q lumens, then the illumination on a surface perpendicular to the radius at a distance r is E = Q/4πr2. If we express r in metres, we get lux, if in feet, ft-cd. You can use this formula to select light bulbs for illumination, since the total number of lumens emitted is usually shown on the box. If you know r and the desired illumination, then you can select a bulb giving the required Q. Of course, a bulb is not isotropic, but this is close enough for government work.
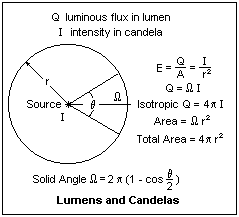 It is convenient to define the luminous intensity of an isotropic source as I = Q/4π, for then E = I/r2, a very simple formula. If Q is in lumens, then I is in candela, cd. This used to be called candlepower. In fact, 1 cd is roughly the intensity of a normal candle (it was originally the intensity of a spermaceti candle of six to the pound burning 120 grains per hour). These things are illustrated in the diagram at the left. Now, 4π is the total solid angle around a point, so we can extend the definition of I to I = dQ/dΩ, where Ω is the solid angle (surface area divided by the square of the distance). Now we can specify a source that is not isotropic by giving its luminous intensity in various directions. This is what is done with LED's. The solid angle included in a cone of angle θ (total angle) is given by the formula in the diagram. The mean spherical candlepower (MSCP) of a lamp is its total flux Q divided by 4π. A 60 W tungsten bulb has about 70 cp.
It is convenient to define the luminous intensity of an isotropic source as I = Q/4π, for then E = I/r2, a very simple formula. If Q is in lumens, then I is in candela, cd. This used to be called candlepower. In fact, 1 cd is roughly the intensity of a normal candle (it was originally the intensity of a spermaceti candle of six to the pound burning 120 grains per hour). These things are illustrated in the diagram at the left. Now, 4π is the total solid angle around a point, so we can extend the definition of I to I = dQ/dΩ, where Ω is the solid angle (surface area divided by the square of the distance). Now we can specify a source that is not isotropic by giving its luminous intensity in various directions. This is what is done with LED's. The solid angle included in a cone of angle θ (total angle) is given by the formula in the diagram. The mean spherical candlepower (MSCP) of a lamp is its total flux Q divided by 4π. A 60 W tungsten bulb has about 70 cp.
My green LED is specified as 10 cd in an angle of 15°. This specification is definitely not of the MSCP, but of radiation only in the specified cone. The solid angle is 0.0538 sr (steradian), so the luminous flux emitted in this cone is Q = 0.538 lm. The LED takes 20 mA at 3.0 V, or 0.06 W, so the luminous efficiency is about 9 lm/W. There seems to be a good deal of light going elsewhere, but this efficiency is of the same order as that of a tungsten bulb.
Now we must find a way to specify color. A good way to do this was found by the CIE (Commission International d'Éclairage) some years ago. Just as we integrated the spectral density with a weighting function y(λ) to find the luminous flux Y, we find two additional quantities X and Z by using weighting factors x(λ) and z(λ). These quantities are tabulated in the Handbook of Chemistry and Physics. Very roughly, X measures redness and Z measures blueness, while Y is principally greenness. Finding these quantities required a great deal of psychophysical experimentation, but using them is straightforward. Any light can be expressed as X, Y and Z. Two lights with the same X, Y and Z will be perceived identically, however different their spectra may be. This is called a mesomeric match.
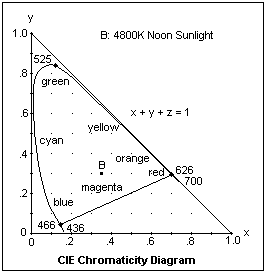 Y gives us the luminous flux, but to specify color independently of brightness we must normalize the parameters. Define x = X/(X+Y+Z), y = Y/(X+Y+Z), z = Z/(X+Y+Z). Since x + y + z = 1, there are only two independent variables to specify color. In a color TV signal, we split the information up is exactly the same way, with a main luminance signal, and two chrominance signals to specify color. The variables x and y can be plotted on rectangular axes, as shown at the right. Along the line from y = 1 to x = 1, z = 0, while at the origin, z = 1. The horseshoe-shaped line is the line of spectral colors, which are the most saturated possible. Note that practically the whole green-red sequence has z = 0, while the green-blue sequence has x = 0, approximately. Any point within the curve represents a possible color. The point B represents noon daylight, a thermal temperature of 4800K, which is perceived as white in daylight. Tungsten light at 2848K is represented by another point, A (not shown). Average daylight at 6500K is represented by a third point, C. These are called standard illuminants. With general tungsten illumination, this light is perceived as white. If you consider any point (x,y), the dominant hue is found by drawing a line from the illuminant (say, point B) through the point (x,y) and extending it to the boundary curve. The intersection is the dominant wavelength.
Y gives us the luminous flux, but to specify color independently of brightness we must normalize the parameters. Define x = X/(X+Y+Z), y = Y/(X+Y+Z), z = Z/(X+Y+Z). Since x + y + z = 1, there are only two independent variables to specify color. In a color TV signal, we split the information up is exactly the same way, with a main luminance signal, and two chrominance signals to specify color. The variables x and y can be plotted on rectangular axes, as shown at the right. Along the line from y = 1 to x = 1, z = 0, while at the origin, z = 1. The horseshoe-shaped line is the line of spectral colors, which are the most saturated possible. Note that practically the whole green-red sequence has z = 0, while the green-blue sequence has x = 0, approximately. Any point within the curve represents a possible color. The point B represents noon daylight, a thermal temperature of 4800K, which is perceived as white in daylight. Tungsten light at 2848K is represented by another point, A (not shown). Average daylight at 6500K is represented by a third point, C. These are called standard illuminants. With general tungsten illumination, this light is perceived as white. If you consider any point (x,y), the dominant hue is found by drawing a line from the illuminant (say, point B) through the point (x,y) and extending it to the boundary curve. The intersection is the dominant wavelength.
The three points marked 466, 525 and 626 represent blue, green and red LED's selected to form a triangle including as much of the diagram as possible. Any color represented by a point within this triangle can be obtained by a mixture of the three lights. The LED's are not monochromatic, but their actual representative points will not be far from those shown. We should not expect to get spectrally pure colors by mixing impure colors, and indeed we cannot. These three LED's actually give a better coverage than the traditional three stimuli, selected from the spectrum of a mercury lamp. The mixing cannot be done by projecting the light from the LED's onto a diffusing surface, because the optical quality of the beams is very poor and uneven. It is much better to use a block of paraffin wax in which the LED's are embedded. The wax scatters light very strongly (it appears milky under normal illumination) without absorbing it, so the three colors will mix evenly. It is very easy to observe red and green mixing to form yellow, or red and blue to form magenta, or all three colors to make a good white.
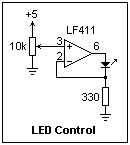 The LED's can be controlled by circuits like the one at the left. The current through the LED can be accurately and reproducibly adjusted with the potentiometer. The 330Ω resistor gives currents up to 15 mA, which the LF411 can supply, and which are sufficient to light the LED's brightly. For making quantitative measurements, a Joly photometer is convenient. This consists of two blocks of paraffin wax, separated by a sheet of aluminum foil. One block should have the LED's, while the other can be illuminated by selected sources. The LED's are adjusted until the two sides appear identical. It would require a painstaking series of measurements to calibrate the LED's in terms of the CIE coordinates, but in principle it can be done. The route is to note the potentiometer settings required for a match, then to express these as X, Y and Z from the results of tests on each LED separately, and finally to calculate x and y. Note that it is not required to make a calibration in terms of 680 lm/W, since only relative values enter.
The LED's can be controlled by circuits like the one at the left. The current through the LED can be accurately and reproducibly adjusted with the potentiometer. The 330Ω resistor gives currents up to 15 mA, which the LF411 can supply, and which are sufficient to light the LED's brightly. For making quantitative measurements, a Joly photometer is convenient. This consists of two blocks of paraffin wax, separated by a sheet of aluminum foil. One block should have the LED's, while the other can be illuminated by selected sources. The LED's are adjusted until the two sides appear identical. It would require a painstaking series of measurements to calibrate the LED's in terms of the CIE coordinates, but in principle it can be done. The route is to note the potentiometer settings required for a match, then to express these as X, Y and Z from the results of tests on each LED separately, and finally to calculate x and y. Note that it is not required to make a calibration in terms of 680 lm/W, since only relative values enter.
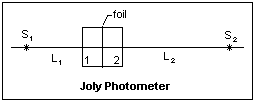 A Joly photometer is sketched at the right. It consists of paraffin wax blocks 1 and 2, separated by aluminum foil, called the photometer head. The wax comes in 1 lb (500 g) packages containing four 3/4" thick blocks. Cut one block in half with a penknife (take care not to break the block), separate the two halves with the foil, and use an elastic band to hold them together. The head is placed between two sources S1 and S2 and moved until the two blocks appear equally bright. Then the intensities of the sources are in the inverse ratio of the squares of the distances L1 and L2, measured (say) to the centers of the blocks. As long as the distances are large compared to the size of the head, to what point they are measured is unimportant. The Bunsen photometer uses a paper screen with a grease spot instead. It is adjusted until the grease spot is as bright as the paper around it on both sides. In the Rumford photometer, the brightness of shadows cast by the two sources of a rod, arranged to be side by side, is compared. The flicker photometer presents two images alternately, and the adjustment is made until the flicker disappears. This kind of photometer is suitable for comparing different colors. A calibrated photodetector can be used to compare physical intensities, but will not necessarily give subjective matches with different spectra. Sometimes, filters are used to give the photodetector the same response as the eye.
A Joly photometer is sketched at the right. It consists of paraffin wax blocks 1 and 2, separated by aluminum foil, called the photometer head. The wax comes in 1 lb (500 g) packages containing four 3/4" thick blocks. Cut one block in half with a penknife (take care not to break the block), separate the two halves with the foil, and use an elastic band to hold them together. The head is placed between two sources S1 and S2 and moved until the two blocks appear equally bright. Then the intensities of the sources are in the inverse ratio of the squares of the distances L1 and L2, measured (say) to the centers of the blocks. As long as the distances are large compared to the size of the head, to what point they are measured is unimportant. The Bunsen photometer uses a paper screen with a grease spot instead. It is adjusted until the grease spot is as bright as the paper around it on both sides. In the Rumford photometer, the brightness of shadows cast by the two sources of a rod, arranged to be side by side, is compared. The flicker photometer presents two images alternately, and the adjustment is made until the flicker disappears. This kind of photometer is suitable for comparing different colors. A calibrated photodetector can be used to compare physical intensities, but will not necessarily give subjective matches with different spectra. Sometimes, filters are used to give the photodetector the same response as the eye.
 Do not omit to inspect your video screen with a 10X magnifying lens. The red, green and blue dots are amazing. Think what was required to get them all in the right places! The figure at the right has red, green and blue discs to examine. Unfortunately, it is not possible to overlap the discs and see the mixed colors with what is available in HTML. These are the additive primaries. The subtractive primaries are cyan, yellow and magenta, which you can see in color transparencies. Unless you choose them very carefully, mixing pigments just gives you an obscure brown, as many school children have discovered.
Do not omit to inspect your video screen with a 10X magnifying lens. The red, green and blue dots are amazing. Think what was required to get them all in the right places! The figure at the right has red, green and blue discs to examine. Unfortunately, it is not possible to overlap the discs and see the mixed colors with what is available in HTML. These are the additive primaries. The subtractive primaries are cyan, yellow and magenta, which you can see in color transparencies. Unless you choose them very carefully, mixing pigments just gives you an obscure brown, as many school children have discovered.
References
The LED's I used were Hosfelt 25-365 (466 nm, 6 cd), 25-377 (525 nm, 10 cd) and 25-405 (626 nm 8 cd). The relative visibilities were 0.074, 0.793 and 0.321, respectively. These are relatively expensive LED's, and come in a clear T-1-1/4 encapsulation.
Return to Electronics Index
Composed by J. B. Calvert
Created 26 May 2002
Last revised 28 May 2002
 It is convenient to define the luminous intensity of an isotropic source as I = Q/4π, for then E = I/r2, a very simple formula. If Q is in lumens, then I is in candela, cd. This used to be called candlepower. In fact, 1 cd is roughly the intensity of a normal candle (it was originally the intensity of a spermaceti candle of six to the pound burning 120 grains per hour). These things are illustrated in the diagram at the left. Now, 4π is the total solid angle around a point, so we can extend the definition of I to I = dQ/dΩ, where Ω is the solid angle (surface area divided by the square of the distance). Now we can specify a source that is not isotropic by giving its luminous intensity in various directions. This is what is done with LED's. The solid angle included in a cone of angle θ (total angle) is given by the formula in the diagram. The mean spherical candlepower (MSCP) of a lamp is its total flux Q divided by 4π. A 60 W tungsten bulb has about 70 cp.
It is convenient to define the luminous intensity of an isotropic source as I = Q/4π, for then E = I/r2, a very simple formula. If Q is in lumens, then I is in candela, cd. This used to be called candlepower. In fact, 1 cd is roughly the intensity of a normal candle (it was originally the intensity of a spermaceti candle of six to the pound burning 120 grains per hour). These things are illustrated in the diagram at the left. Now, 4π is the total solid angle around a point, so we can extend the definition of I to I = dQ/dΩ, where Ω is the solid angle (surface area divided by the square of the distance). Now we can specify a source that is not isotropic by giving its luminous intensity in various directions. This is what is done with LED's. The solid angle included in a cone of angle θ (total angle) is given by the formula in the diagram. The mean spherical candlepower (MSCP) of a lamp is its total flux Q divided by 4π. A 60 W tungsten bulb has about 70 cp. Y gives us the luminous flux, but to specify color independently of brightness we must normalize the parameters. Define x = X/(X+Y+Z), y = Y/(X+Y+Z), z = Z/(X+Y+Z). Since x + y + z = 1, there are only two independent variables to specify color. In a color TV signal, we split the information up is exactly the same way, with a main luminance signal, and two chrominance signals to specify color. The variables x and y can be plotted on rectangular axes, as shown at the right. Along the line from y = 1 to x = 1, z = 0, while at the origin, z = 1. The horseshoe-shaped line is the line of spectral colors, which are the most saturated possible. Note that practically the whole green-red sequence has z = 0, while the green-blue sequence has x = 0, approximately. Any point within the curve represents a possible color. The point B represents noon daylight, a thermal temperature of 4800K, which is perceived as white in daylight. Tungsten light at 2848K is represented by another point, A (not shown). Average daylight at 6500K is represented by a third point, C. These are called standard illuminants. With general tungsten illumination, this light is perceived as white. If you consider any point (x,y), the dominant hue is found by drawing a line from the illuminant (say, point B) through the point (x,y) and extending it to the boundary curve. The intersection is the dominant wavelength.
Y gives us the luminous flux, but to specify color independently of brightness we must normalize the parameters. Define x = X/(X+Y+Z), y = Y/(X+Y+Z), z = Z/(X+Y+Z). Since x + y + z = 1, there are only two independent variables to specify color. In a color TV signal, we split the information up is exactly the same way, with a main luminance signal, and two chrominance signals to specify color. The variables x and y can be plotted on rectangular axes, as shown at the right. Along the line from y = 1 to x = 1, z = 0, while at the origin, z = 1. The horseshoe-shaped line is the line of spectral colors, which are the most saturated possible. Note that practically the whole green-red sequence has z = 0, while the green-blue sequence has x = 0, approximately. Any point within the curve represents a possible color. The point B represents noon daylight, a thermal temperature of 4800K, which is perceived as white in daylight. Tungsten light at 2848K is represented by another point, A (not shown). Average daylight at 6500K is represented by a third point, C. These are called standard illuminants. With general tungsten illumination, this light is perceived as white. If you consider any point (x,y), the dominant hue is found by drawing a line from the illuminant (say, point B) through the point (x,y) and extending it to the boundary curve. The intersection is the dominant wavelength. The LED's can be controlled by circuits like the one at the left. The current through the LED can be accurately and reproducibly adjusted with the potentiometer. The 330Ω resistor gives currents up to 15 mA, which the LF411 can supply, and which are sufficient to light the LED's brightly. For making quantitative measurements, a Joly photometer is convenient. This consists of two blocks of paraffin wax, separated by a sheet of aluminum foil. One block should have the LED's, while the other can be illuminated by selected sources. The LED's are adjusted until the two sides appear identical. It would require a painstaking series of measurements to calibrate the LED's in terms of the CIE coordinates, but in principle it can be done. The route is to note the potentiometer settings required for a match, then to express these as X, Y and Z from the results of tests on each LED separately, and finally to calculate x and y. Note that it is not required to make a calibration in terms of 680 lm/W, since only relative values enter.
The LED's can be controlled by circuits like the one at the left. The current through the LED can be accurately and reproducibly adjusted with the potentiometer. The 330Ω resistor gives currents up to 15 mA, which the LF411 can supply, and which are sufficient to light the LED's brightly. For making quantitative measurements, a Joly photometer is convenient. This consists of two blocks of paraffin wax, separated by a sheet of aluminum foil. One block should have the LED's, while the other can be illuminated by selected sources. The LED's are adjusted until the two sides appear identical. It would require a painstaking series of measurements to calibrate the LED's in terms of the CIE coordinates, but in principle it can be done. The route is to note the potentiometer settings required for a match, then to express these as X, Y and Z from the results of tests on each LED separately, and finally to calculate x and y. Note that it is not required to make a calibration in terms of 680 lm/W, since only relative values enter. A Joly photometer is sketched at the right. It consists of paraffin wax blocks 1 and 2, separated by aluminum foil, called the photometer head. The wax comes in 1 lb (500 g) packages containing four 3/4" thick blocks. Cut one block in half with a penknife (take care not to break the block), separate the two halves with the foil, and use an elastic band to hold them together. The head is placed between two sources S1 and S2 and moved until the two blocks appear equally bright. Then the intensities of the sources are in the inverse ratio of the squares of the distances L1 and L2, measured (say) to the centers of the blocks. As long as the distances are large compared to the size of the head, to what point they are measured is unimportant. The Bunsen photometer uses a paper screen with a grease spot instead. It is adjusted until the grease spot is as bright as the paper around it on both sides. In the Rumford photometer, the brightness of shadows cast by the two sources of a rod, arranged to be side by side, is compared. The flicker photometer presents two images alternately, and the adjustment is made until the flicker disappears. This kind of photometer is suitable for comparing different colors. A calibrated photodetector can be used to compare physical intensities, but will not necessarily give subjective matches with different spectra. Sometimes, filters are used to give the photodetector the same response as the eye.
A Joly photometer is sketched at the right. It consists of paraffin wax blocks 1 and 2, separated by aluminum foil, called the photometer head. The wax comes in 1 lb (500 g) packages containing four 3/4" thick blocks. Cut one block in half with a penknife (take care not to break the block), separate the two halves with the foil, and use an elastic band to hold them together. The head is placed between two sources S1 and S2 and moved until the two blocks appear equally bright. Then the intensities of the sources are in the inverse ratio of the squares of the distances L1 and L2, measured (say) to the centers of the blocks. As long as the distances are large compared to the size of the head, to what point they are measured is unimportant. The Bunsen photometer uses a paper screen with a grease spot instead. It is adjusted until the grease spot is as bright as the paper around it on both sides. In the Rumford photometer, the brightness of shadows cast by the two sources of a rod, arranged to be side by side, is compared. The flicker photometer presents two images alternately, and the adjustment is made until the flicker disappears. This kind of photometer is suitable for comparing different colors. A calibrated photodetector can be used to compare physical intensities, but will not necessarily give subjective matches with different spectra. Sometimes, filters are used to give the photodetector the same response as the eye. Do not omit to inspect your video screen with a 10X magnifying lens. The red, green and blue dots are amazing. Think what was required to get them all in the right places! The figure at the right has red, green and blue discs to examine. Unfortunately, it is not possible to overlap the discs and see the mixed colors with what is available in HTML. These are the additive primaries. The subtractive primaries are cyan, yellow and magenta, which you can see in color transparencies. Unless you choose them very carefully, mixing pigments just gives you an obscure brown, as many school children have discovered.
Do not omit to inspect your video screen with a 10X magnifying lens. The red, green and blue dots are amazing. Think what was required to get them all in the right places! The figure at the right has red, green and blue discs to examine. Unfortunately, it is not possible to overlap the discs and see the mixed colors with what is available in HTML. These are the additive primaries. The subtractive primaries are cyan, yellow and magenta, which you can see in color transparencies. Unless you choose them very carefully, mixing pigments just gives you an obscure brown, as many school children have discovered.