Electromagnetic Waves in Crystals

1. Plane Waves
2. Electromagnetic Waves in crystals; conical refraction
3. Energy and the Index Ellipsoid
4. Mica and thin-film interference; Pohl's demonstration; polarization; Newton's Rings; Fresnel's Formulas
5. Interference in Highly Convergent Light
6. References

A magnitude varying sinusoidally with time is conveniently expressed by a multiplicative exponential function e^±iφ = cos φ ± sin &phi, where φ is the phase, which depends linearly on the time t. An increase in φ by 2π corresponds to a complete cycle of variation. If a cycle is completed in a time interval T, then the phase is 2πt/T. In other words, the frequency f is 1/T cycles per second, or Hz. The physical quantity is usually taken as the real part, cos φ. It is not important whether the plus or minus sign appears before the phase (it does not affect the real part), but it is important to be consistent in the notation, since it does affect phase differences. The negative sign will be used here to be consistent with Born and Wolf.

Quantities expressed exponentially are easy to add and subtract, shift in phase, and, most importantly, can be differentiated and integrated very simply. The time derivative is expressed by multiplication by -i(2π/T) = -i(2πf) = -iω. The angular frequency ω = 2πf. Adding and subtracting can be done with the familiar phasor diagrams, which reduce this to vector addition or subtraction. Multiplication by a complex number ae^ψ multiplies the length of the phasor representing the sinusoidal quantity by a and rotates it anticlockwise by an angle ψ. Of course, a and ψ are real quantities. Care must be taken when multiplying exponential quantities: what is intended is often the multiplication of the real quantities, as in the calculation of power.

A plane wave is a sinusoidal quantity whose phase is constant over plane surfaces, called the wavefronts. A plane can be specifed by a normal vector s as s·r = d, where s is the unit wave normal vector, r is the position vector from the origin O, and d is the closest (i.e. normal) distance from the origin to the plane. The sinusoidal function executes a complete cycle when the distance of the plane from the origin increases by an amount λ, called the wavelength. That is, phase = -2πd/λ, if we consider that phases ahead in the wave are progressively earlier. The space and time variations are, then, related by φ = (2π/T)t - (2π/λ)d. Considering a point of constant phase 0 moving with the wave, d = (λ/T)t. The phase velocity of the wave is v = λ/T = λf. If c is a reference velocity, then the index of refraction n = c/v.

A plane wave function is easily differentiated with respect to the space coordinates. For example, ∂/∂x is equivalent to multiplication by -i(2π/λ)s_x or -i(ωn/c)s_x. The gradient operator (del) becomes multiplication by -i(ωn/c)s. Because browsers lack the del, we will use Ð instead.

The fields in an electromagnetic wave are the electric field E and the magnetic induction B. It is convenient to introduce two other fields, the electric displacement D, which is E + 4πP, where P is the electric dipole moment per unit volume, and the magnetic intensity H, which is B - 4πM, where M is the magnetic dipole moment per unit volume. We shall assume that M is proportional to B, so that B = μH, but normally take the permeability μ = 1 while keeping μ in the equations for generality.

In an isotropic medium, for all practical field strengths, P = χE is the induced dipole moment, where the permittivity χ is a constant. Then, D = (1 + 4πχ)E = εE, where ε is the dielectric constant. In an anisotropic medium, such as a crystal, we may still assume that the polarization is a linear function of the electric field, but with a more general relation D_i = ε_ijE_j (sum over i and j from 1 to 3) with nine constants. It can be shown that the matrix ε_ij must be symmetric, so that there are actually only six constants. Finally, we can find a coordinate system that diagonalizes the matrix, so only the three principal dielectric constants ε_k, k = 1, 2, 3 remain, so that D_k = ε_kE_k, k = 1, 2, 3. If these are equal, we have the isotropic case mentioned above, with D and E in the same direction and proportional to each other. If they are not equal, then D and E will in general be in different directions.

Now let us find the relations between the field vectors and the wave normal from Maxwell's equations. The linearity of the equations makes this very easy; there will be no differential equations to solve! First, зB = 0 becomes s·B = 0, which means that B is perpendicular to s, and so lies in the wavefront. Next, зD = 0, since we assume there are no free charges in the region. Therefore, s·D = 0, so D also lies in the wavefront. If there are also no currents (conductivity of the medium zero), cÐ×H = -∂D/∂t. This becomes ns×H = -D, showing that D is perpendicular to both H and s. That is, s, H and D form a right-angled triplet. The relation between the magnitudes of D and H is also given. Finally, cÐ×E = -∂B/∂t becomes ns×E = μH. The field vectors are shown in the diagram. The constant c, the speed of light in a vacuum, has been introduced naturally through the units, which are the traditional cgs units here.

Eliminating H between the two cross product equations gives D = -(n²/μ)[s×(s×E)]. Expanding the triple cross product, we have D = (n²/μ)[E - s(s·E)]. The vector in square brackets is just the component of E along D, which is shown in the figure above. This is a very significant equation, since using the known relation between E and D we can determine the phase velocity of the wave. To show this, let's consider the case of an isotropic medium in which D = εE. In this case, we also have s·E = 0, so we get simply εE = (n²/μ)E, or n = √(με), giving the phase velocity v = c/√(με). Since μ is usually unity, we have Maxwell's relation n = √ε that relates the phase velocity to the dielectric constant. Of course, this is the dielectric constant at the frequency of the wave, which is around 10¹⁵ Hz, and not the static dielectric constant, which is normally much greater.

The Poynting vector S= (c/4π)(E×H) is also shown. It defines the unit ray vector t which gives the direction of energy flow. If E and D are not in the same direction, the wave normal and the ray vector make an angle α with each other. The ray velocity v' is defined by v' = S/w, where w is the energy density in the wave. From the diagram, v = v' cos α. The ray index n' is defined analogously to n, as n' = c/v', and n' = n cos α.

The component of E along D is (E·D)D/D², from which we find n² = μD²/E·D. Then, n'² = n² cos²α = μE·D/E². But, the component of D along E is (D·E)(E)/E², or (n'²/μ)E. This gives us a second equation for determining velocities in terms of t instead of s: E = (μ/n'²)[D - t(t·D)]. Solving this equation will give the ray velocity for any unit ray vector t, while solving the other equation will give the phase velocity for any wavefront normal vector.

Let's solve the ray equation first. Use principal axes, which we can take to be the x,y,z or 1,2,3 axes. Let the x- or 1-axis correspond to the smallest of the principal dielectric constants ε_k, the z- or 3-axis to the largest, and the y- or 2-axis to the intermediate value. The corresponding velocities v_k = c/√ε_k are in the reverse order of magnitude. Since E_k = D_k/ε_k, we can solve for D_k to find D_k = t_k(t·D)/(1 - n'²/με_k) for k = 1,2,3. The trick is to multiply each equation by t_k and sum over k. The dot product can then be cancelled out, so we get Σ[t_k²/(1 - v_k²/v'²)] = 1. This equation will give us the ray velocities v', but a more convenient form of the equation can be obtained. Just subtract Σt_k² = 1 from both sides of the equation. Then Σt_k²/(1/v'² - 1/v_k²) = 0, which is Fresnel's equation of wave normals. Fresnel derived it on a mechanical theory of light; it is much easier to do it this way.

To solve the equation, first multiply out the denominators. I'll leave this to the reader. The result is a quadratic equation in v'², which gives us two roots corresponding to different polarizations, and for each root solutions of opposite signs for v', corresponding to rays in opposite directions. This is troublesome to do in general, and numerical solutions are not very enlightening. What is usually done is to consider the special cases of rays in the coordinate planes. For example, let t_y = 0, so the ray will be in the xz-plane. Then we have (1/v'² - 1/v₂²) [t₁²(1/v'² - 1/v₃²) + t₃(1/v'² - 1/v₁²)] = 0. Equating each factor separately to zero, we find v' = v₂, and, writing x = v't₁ and z = t₃, (x/v₃)² + (z/v₁)² = 1. That is, we find a circle and an ellipse. For any direction of t, there are two possibilities.

In the xz-plane, the circle and ellipse intersect at four points. If you repeat the analysis for the xy- and yz planes, the ellipse will lie within the circle, or the circle within the ellipse, without intersecting. The circle is not a cross-section of a sphere, and the ellipse not a cross-section of an ellipsoid. It is very difficult to visualize the general shape of the wave surface. This wave surface is the closest analog to a Huygens's wavelet, but is really not that. The wavefront is parallel to the tangent to the wave surface at the point where the ray intersects it. A normal from the wavefront to the origin is the direction of the wave normal, and the point of intersection of this normal with the wavefront is a point on the normal wave surface. These points define a surface that is pedal to the ray surface, and turns out to be the solution for the equation in terms of the ray normal s. These two surfaces are often confused, but must be carefully distinguished. The normal wave surfaces on the coordinate planes are a circle and an oval that may look elliptical, but is not. It is the pedal curve of the ray ellipse.

An optic axis is a wave normal direction in which all polarizations have the same phase velocity. It lies in the plane in which the ray surfaces intersect, the xz-plane. The common tangent to the ellipse and the circle are tangent at points where the two rays meet a common wavefront, and so have the same phase velocity. The optic axis is in the direction of the wave normal at the circle. The normal wave surfaces will intersect at a point in this direction. A difficult analysis shows that not only these two rays have the same wave normal, but an infinite number. The tangent plane does not meet the ray surface at just two points, but at all points on a ring of which these two points determine a diameter. To one wave normal, then, corresponds a cone of rays, which give rise to the strange phenomenon of internal conical refraction. Notice that the axis of this cone is along the ray to the point of intersection of the two ray surfaces, which is called the ray axis. Curiously, it is also the axis of a cone of wave normals corresponding to the same ray, and gives rise to external conical refraction.

Conical refraction was predicted in 1832 by W. R. Hamilton on the basis of Fresnel's theory, and observed by H. Lloyd in 1833 in plates of aragonite (orthorhombic CaCO₃) cut normal to the optic axis. If the experiment is carefully done, the circle of light in internal conical refraction is divided by a central dark ring. Conical refraction was a convincing proof of Fresnel's theory.

The Poynting vector (c/4π)(E&mult;H) can be interpreted as the energy flux in the electromagnetic field. The light field varies so rapidly in time that only average values are observed. The instantaneous values may be replaced by their maximum values or amplitudes, and taking the time average of a quadratic product is equivalent to division by 2 (average value of cos²ωt = 1/2). For simplicity, we shall use instantaneous values, realizing that the time average is easily found.

Let us take div(E&mult;H) = H·curl E - E·curl H = -(1/c)(H·∂B∂t + E·∂D/∂t. If B and H are linearly related, as by B = μH, and the same holds for D and E, even if we have a dielectric constant tensor instead of the simple relation D = εE, the terms on the right become -(1/2c)d/dt(H·B + E·D). Finally, then, we have the equation div[(c/4π)(E&mult;H)] + (d/dt)(H·B/8π + E·D/8π) = 0. If this is applied to a volume V with a surface S, it says that the flux of energy out of V is equal to the rate of decrease of the field energy within V.

Let us assume for the moment that we are dealing with an isotropic medium of dielectric constant ε Maxwell's equations show that the relation between the magnitudes of H and D is nH = D, where the index of refraction n = √(με). Then, the product ED = (n²/με) HB = HB. Therefore, the electric and magnetic energy densities are equal. We expect that this will hold for a nonisotropic medium as well.

The total average field energy w can then be expressed as w = ΣD_k²/8πε_k. If we set x_k = D_k/√(8πw), this equation becomes Σ x_k²/ε_k = 1, which is an ellipsoid with axes √(ε_k, k = 1,2,3. The dielectric constants ε here are those valid at the high frequencies of light waves, not the static values, which may be much larger. This will be called the index ellipsoid here, to emphasize that the lengths of its axes are the indices of refraction. Many authors call it the optical indicatrix, which is uninformative; Born and Wolf say ellipsoid of wave normals, which sounds like something else, while Jenkins and White call it the dielectric ellipsoid, which is not too bad. It is really an energy surface expressed in terms of D. We usually let the 1- or x- axis have the smallest index, the 3- or z-axis the largest index, and the 2- or y-axis the intermediate value. Phase velocity is, of course, inversely related to the index of refraction, so the velocities are in the opposite order.

The index ellipsoid is sketched in the diagram at the right. Let s be a wave normal vector, and imaging a plane perpendicular to it through the origin, which will cut the ellipsoid in an ellipse. Let r be a vector from the origin to this ellipse. By finding the extrema of the length r of this vector under the conditions that it lie on the plane normal to s and on the index ellipsoid as well (See Born and Wolf, p. 671, where this is done by the method of Lagrangian multipliers), we determine the directions D and D" of the displacement vector in the corresponding waves. Moreover, the lengths of the vectors r = n/√μ give the corresponding phase velocities. For example, suppose the wave normal is in the z-direction. Then the displacement vectors are along the x- and -axes, and the lengths of the radii are √ε_x and √ε_y, so the phase velocities are v' = c/√(με_x and v" = c/√(με_y, just those which we would use to label the axes. It is not easy to calculate with the index ellipsoid, but it is an excellent graphic aid.

The same thing can be done with the energy ellipsoid expressed in terms of E. Now the lengths of the axes are the reciprocals of the indices of refraction. The ray vector t replaces the wave normal s, and the square of the length from the origin is √μ/n_r², giving the ray velocity.

There appears to be no easy graphical way to find the ray vectors t corresponding to a given s, or vice versa. An algebraic solution is given by Born and Wolf, but it is not simple. The two D vectors obtained for a given wave normal do not, in general, correspond to the same ray vector. If the D vectors are found, then the corresponding E vectors can be determined, using the dielectric constants. Using the other D" vector in each case, which is perpendicular to s and D', the ray direction can be determined by taking the cross product.

Mica is a common mineral that appears in many related compositions, all characterized by perfect cleavage into thin, flexible plates that is the basis of its utility in optics. The usual mica is the variety muscovite, named not for a location where it was collected, but for its common use in windows in medieval Moscow, instead of glass. It is clear and transparent, unlike most other micas. It crystallizes in the monoclinic system, class 2/m, so it is optically biaxial. The 2-fold axis is usually chosen as the crystallographic b- or y-axis, perpendicular to the plane of symmetry containing the a- or x-axis and the c- or z-axis. The cleavage is in the (001) direction, so cleavage plates contain the crystallographic y-axis. The axial angle β of the x-axis with respect to the z-axis is close to 90°, so mica is almost orthorhombic, and the axes are nearly an orthogonal triplet.

The dielectric principal axes are labelled somewhat differently. The dielectric x-axis is the crystallographic z-axis, normal to the cleavage. The y-axis is the same as the crystallographic y-axis, constrained to lie along the 2-fold axis. The z-axis is about perpendicular to the x- and y-axes. I actually do not know whether the intermediate index of refraction belongs to the y-axis; it may belong to the z-axis as we have just defined them, so the designations y and z may have to be interchanged. The least index surely belongs to the x-axis, where the vibrations are perpendicular to the cleavage. The indices, according to Jenkins and White, are 1.5601, 1.5936 and 1.5977. Since mica is a variable natural product, these values may vary somewhat. In a cleavage plate, we may assume the fast and slow axes are at right angles and have the last two values. If we use mica as a transparent plate, then we may take the index as about 1.59. It is a negative biaxial crystal, since the smallest index belongs to the x direction. Take care to distinguish the crystallographic and optical axis designations.

Chemically, muscovite is KAl₃Si₃O₁₀(OH)₂, a phyllosilicate. It is soft, not decomposed by acids, and resists heat. It is a good electrical insulator, and is used as a capacitor dielectric. Its static dielectric constant is 5.6 - 6.6, and its density is 2.76 - 3.1 g/cc. Large crystals are approximately hexagonal (110)-face prisms. A sharp blow with a blunt object on a cleavage plate gives a six-rayed percussion figure. The most prominent split is parallel to the plane of symmetry (perpendicular to the y-axis). Used as a stove window or flexible transparent screen, it was called isinglass.

Mica is very useful in experiments on interference and polarization. It can be cleaved into plates 0.01 mm thick which are still relatively robust. Cleaved plates are also uniform in thickness. Two dielecric principal axes are at right angles, with a difference in indices small enough that wave plates (see below) are not too thin. Even an 0.01 mm plate is 27 wavelengths thick at 589 nm. The number of wavelengths in a thickness t is nt/λ, where n is the index of refraction and λ is the wavelength in vacuum.

A good experiment is to cover half of one of the slits in a two-slit diffraction experiment with a thin mica plate. With present-day sources, there is plenty of intensity even with slits. The mica introduces an additional optical path length of (n - 1)t, and so shifts the zero-order fringe b a distance x = (D/d)(n - 1)t, where D is the distance to the screen and d the slit spacing. If monochromatic light is used, all fringes look the same and it would be difficult to find the zero-order fringe displacement. The solution to this is to use white light, which gives a distinctive zero-order bright fringe surrounded by a few colored fringes. This allows the position of the zero-order fringe to be marked for comparison with the zero-order fringe without the mica. It is possible to find the thickness of the mica plate in this way, which otherwise is difficult to measure.

Pohl's demonstration of interference in a thin film is very impressive and easy to set up. The arrangement is shown in the Figure. Light from a bright Na or Hg arc is reflected from a mica plate of thickness about 0.04 - 0.07 mm onto a screen a few metres away. A shield prevents the observer from being dazzled. A great number of circular fringes of high visibility (contrast between maximum and minimum) are observed. (A green filter should be used with a Hg arc.)

I used a Pasco OS-9287B Na lamp and a 4" x 5" sheet of stove mica about 0.1 mm thick, just as it came from the supplier. The mica was about 30 cm from the source, and the fringes were viewed on a wall about 155 cm from the mica. The housing for this lamp is large, so it was only possible to reflect the light around one side of it. The second opening on the back of the housing must be blocked. Circular two-beam fringes of good visibility were seen, with a spacing of about 23 mm. Note that there must be sufficient spread in the light to produce fringes. No fringes are seen if a small aperture is used instead.

Differentiating the thin film formula (see below) 2nd cos r = mλ, we find 2nd sin r dr = dmλ, or, with dm = 1, dr = λ/2nd sin r. Now, di = (n cos r/cos i) dr from Snell's Law, so di = λ/2d cos i tan r. Estimating i = 20°, then r = 12.42° and di = .0142 rad. At a distance of 1550 mm, this gives a fringe spacing of 22 mm, agreeing with the observed value.

Another familiar example of interference in light reflected from thin films is the colors seen in puddles in the road, when a drop of oxidized motor oil has fallen into them. These have the colors of white-light fringes. The oil film is a micron thick or less, only a wavelength or two, in this case.

The theory of thin film fringes is illustrated at the left. Light is incident on the surface of the film at an angle of incidence i. At A its amplitude is divided into two parts. Some is reflected at the same angle i, while the majority is transmitted into the film at an angle of refraction r. At point F the amplitude is again divided, with about the same fraction as at A reflected, while most is transmitted into the third medium. We assume the film has an index of refraction n, with air or vacuum on both sides. The light reflected at F strikes the upper surface at B, and is mostly transmitted on at an angle i with the normal. We neglect the small amount of light reflected at B in this case. The result is that two beams are reflected, of about the same intensity. The second beam travels an extra distance that we shall now calculate. While the first beam moves from A to D, the second beam moves from C to B. The optical path length is the same on each path, AD = nCB; that is, this is the path length measured in wavelengths. Therefore, the second ray travels an additional distance AFC in the medium of index n. Right triangles AEF and GEF are congruent, so AF = FG. In the right triangle AGC, AFC = GC = AG cos r, or AFC = 2d cos r. The optical path difference is then 2nd cos r. A wave reflected at a rare to dense interface is shifted in phase by 180°, while one reflected at a dense to rare interface is not shifted in phase. This is a general rule applying to mechanical waves as well as to electromagnetic waves. Since the first beam is reflected rare to dense, and the second dense to rare, if the optical path difference is a whole number of wavelengths, then the beams will be 180° out of phase, and will interfere destructively. Therefore, we have: 2nd cos r = mλ (dark fringes). The integer m is the order of the interference. Note that the angle of refraction r appears in the formula, not the angle of incidence i.

If we illuminate a thin film by an extended monochromatic source, whether by transmission or reflection, we will see fringes of a familiar bull's-eye pattern, like those of Newton's Rings. These fringes are seen, for example, in the Michelson interferometer and the Fabry-Perot interferometer, in both of which the spacing d can be quite large. The partial silvering of the Fabry-Perot plates causes multiple reflections, and the interference of these beams results in very narrow fringes, just as it does in the case of a diffraction grating. The two-beam interference in the Michelson interferometer results in fringes with the cos² intensity variation.

Let's set n = 1, as for the Michelson and Fabry-Perot interferometers. For the general case, we may simply replace d by nd. At normal incidence, θ = 0, d = mλ, so m has the generally large value m_o = d/λ. As θ increases, the cosine decreases and so does the order m. Write d(1 - cos θ) = (m_o - m)λ. If θ is small, we expand the cosine to 1 - θ²/2, and then have dθ² = (m_o - m)λ. Therefore, dark fringes (in general) occur for angles θ = a√N, where N is the integer m_o - m and a= √(λ/d) is a constant. The radius of the dark fringes are proportional to the square roots of integers. The reader may want to draw concentric circles with these radii to see the familiar pattern arise. The fringes may be focused on a screen with a lens of focal length f (or on the retina by the eye), so the radii are r = θf.

The visibility of interference fringes may be expressed quantitatively as the ratio V = (Imax - Imin)/(Imax + Imin). If the two interfering waves have equal amplitudes A, then Imax =4A² and Imin = 0, so V = 1 in this case. If the amplitudes are A and 0.1A, V = 0.2. This is also called the modulation or contrast.

The maximum interference order in the Pohl demonstration occurs at the centre, behind the shadow of the lamp housing, and is 2nd/λ. For a 0.05 mm mica sheet, this is about 270 for sodium light. At the rather large angle of i = 30°, r = 18.33° and m = 256.3. We expect, then, about 270 - 256 = 14 dark rings from the centre out to this angle. This is very reasonable, and explains the good appearance of the pattern. Most examples of interference in plates are at near normal incidence.

Conditions with oil films on water, or thin transparent films on solids, are quite different. Illumination is by a broad source of natural light--a bright cloudy sky is ideal. The fringes cannot be projected onto a screen, but appear when the film is viewed. The films are very thin, less than 1 μm, so the interference order is low, as is required for white-light fringes, which require m < 4. In these fringes, interference removes certain bands of wavelengths, and the colour seen is that of the remaining light. Minnaert gives the correspondence between thickness and colour for oil films (pp. 208ff).

Although we speak of oil films, clean oil is hydrophobic and collects in drops, and does not spread into a film. Turpentine does spread into a film, and provides bright colours until it dissolves in the water. Turpentine is produced by distilling pine tar, and consists mostly of pinene, (C₅H₈)₂, a monoterpene consisting of two isoprene units. Its index of refraction is 1.465, so the reflections at the two surfaces are rare-dense and dense-rare as assumed above. Since the index of water is only 1.333, this will be the case for practically all such films. Films on solids may give two rare-dense reflections, so even orders will correspond to bright fringes. This should be noticeable in the observed colours.

The colours in thin films are not in the films themselves, but are produced when the two wavefronts interfere in the eye at the image of the viewed area. Since the film is thin, both rays can easily enter the pupil of the eye. In some cases of interference, the interfering rays may be considerably separated. If they do not both enter the eye, no fringes are seen.

A thin film of air separates the spherical surface of a plano-convex lens and a flat glass plate on which it rests. If h is the distance from the point of contact and r the radius of the lens surface, then the thickness of the film is t = h²/2r. Spherical surfaces on lenses can be made very perfect, so t is accurately given by this formula. The fringes are observed near normal incidence, so the condition for dark rings is m = h²/rλ (n = 1). These are the celebrated Newton's Rings, used for his original description of the interference colours seen in white light. The radius of a dark ring is h = √(mrλ). For sodium light, r = 1.5 m and m = 20, h = 4.2 mm. A 10X microscope would be abou right for viewing this pattern.

Newton's Rings can be seen with only the lens and plate. Observe the reflection of a broad source from near the point of contact, best with some magnification. There are four reflections seen in general; neglect the ones from the upper and lower plane surfaces, and focus on the ones from the thin air film. Probably with some trouble, you will find the small black spot surrounded by a few coloured rings that is unmistakeable. Viewed in monochromatic light, many dark rings will surround the central spot, in accordance with the formula above. The set-up for observing Newton's Rings with a low-power microscope is shown in the figure. A thin glass plate at 45° is used to direct the beam from the light source normally onto the plano-convex lens and optical flat, from where it is reflected into the microscope. A piece of plate glass can be used, but an optical flat is better. I used a slide cover glass for a beamsplitter, held in a saw cut in a dowel pressed into a styrofoam block. The light source may be an incandescent lamp (flashlight), a mercury discharge with filter, or a sodium vapor lamp. It is not too easy to find the pattern, but with some persistence it can be brought into the field of view. Before looking, the glass beamsplitter should be rotated for maximum intensity of the light, and the microscope should be focused on the top of the optical flat, using a marked piece of paper. The patterns in white light and monochromatic light should be compared. If the diameter of a ring is measured, and the order counted out from the centre, the wavelength can be calculated if the radius of the lens surface is known. Unfortunately, micrometer eyepieces are expensive and difficult to locate. If the contact between lens and plate is not perfect, the central disc may appear less black, and even grey. It is important to keep the lens and flat very clean. Note that the microscope should have a working distance of around 3" to allow room for the beamsplitter.

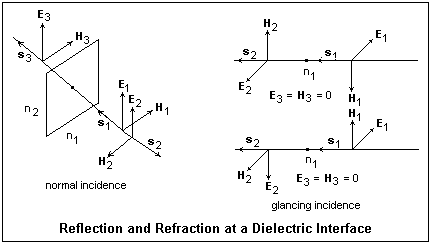The amplitudes and phases of reflected and refracted waves can be found from electromagnetic theory. The general results are known as the Fresnel Equations. Fresnel derived them assuming light was a material wave, a much more difficult matter than using Maxwell's Equations. The complete results are found in many references, such as Born and Wolf, but we shall consider only two special cases, that not only make the analysis clear but correspond to many practical situations. The special cases are those of normal incidence (i = 0°) and glancing incidence (i = 90°), which will free us from a lot of trigonometry that may hide the actual simplicity of the analysis.

First, consider normal incidence. The vector field amplitudes are indicated in the figure. Subscript 1 refers to the incident wave, 2 to the reflected wave, and 3 to the transmitted wave. The magnetic fields are related to the electric fields in these harmonic waves by ns&mult;E = μH. The directions are as shown in the figure, while the magnitudes are related by nE = μH, or H = √(ε/&mu)E. Since there are no free charges or currents at the interface between the media, the tangential electric and magnetic fields must be continuous. We shall not need the boundary conditions on the normal components in this case. It is clear that the tangential fields will be continuous if E₁ + E₂ = E₃ and H₁ - H₂ = H₃. Using the relation between H and E, the second equation becomes n₁(E₁ - E₂) = n₂E₃. These two equations are easily solved for E₂ and E₃ in terms of E₁, with the result that E₂ = [(n₁ - n₂) / (n₁ + n₂)] E₁ and E₃ = [2n₁/(n₁ + n₂)] E₁.

In rare-to-dense reflection, n₂ > n₁. Our result shows that in this case, E₂ will be opposite in sign to E₁. That is, in the diagram it will actually point in the opposite direction to the one we have chosen as positive, which was in the same direction as E₁. For dense-to-rare reflection, there will be no phase inversion.

The case of glancing incidence is even easier. Here, the normal and the incident wave normal vector define the plane of incidence. There are two polarizations, with E parallel to the plane of incidence and E perpendicular to the plane of incidence. This is also the case for arbitrary angle of incidence. For normal incidence, we can choose the plane of incidence as any plane normal to the interface. The diagram applies to both the rare-to-dense and dense-to-rare cases, since the fields in the second medium are zero in both. For dense-to-rare reflection, beyond the angle i given by sin i = 1/n total internal reflection occurs, which requires special treatment. The boundary conditions for rare-to-dense reflection can be satisfied with zero fields in the second medium. This means that the transmitted wave will be very small as we approach i = 90°. Clearly, this happens if The E fields are in the directions shown, so there is a phase reversal for either polarization, which we expect for rare-to-dense reflection. Surprisingly, there is also phase reversal in the dense-to-rare case.

The squares of the quantities we have found will give the relations between the intensities. The sum of the squares of the reflection and transmission ratios is easily seen to be unity, as it should be from conservation of energy. For normal reflection from glass with n=3/2, the amplitude ratio is 1/4, so the intensity ratio is 1/16 or 0.0625, so about 6% of the incident energy is reflected. A glass windowpane reflects about 12% of the incident intensity, not an inconsiderable amount. For reflection from water, where n=4/3, the amplitude ratio is 1/7, the intensity ratio 1/49 or 2%.

The reflectivity at any angle can be expressed as the square of the simple form tan(i - r)/tan(i + r) for E in the plane of incidence, and sin(i - r)/sin(i + r) for E perpendicular to the plane of incidence. When i + r = 90°, the tangent ratio becomes zero: there is no reflection for light of this polarization--it is all transmitted. We have already mentioned this, and this value of i is the Brewster angle, given by tan i = n. Windows at the ends of a gas laser tube are set at the Brewster angle to eliminate reflection losses.

A third use for a thin mica sheet is as a quarter-wave plate, which can convert linear polarization into circular polarization. Circular polarization is the result of light vibrations in the x- and y-directions that are of equal amplitude but 90°, or a quarter-wavelength, out of phase. Imagine you are looking into the light beam, and choose orthogonal x- and y-axes. A vibration x = sin ωt, y = sin (ωt+π/2) = cos ωt describes clockwise rotation of an amplitude vector of unit length, called right-circular polarization, or negative helicity. If the two vibrations are not of the same amplitude, the result is elliptical polarization. If the y vibration is y = sin (ω-π/2) = -cos ωt, the rotation is in the opposite direction, and we have left-circular polarization, or positive helicity. Just as all polarization states can be expressed in terms of the two linear polarizations along the x- and y-axes, they can also be expressed in terms of the two circular polarizations.

A mica sheet has a fast direction (n = 1.5936) at right angles to a slow direction (n = 1.5977). The indices are for yellow sodium light, 589 nm, and, of course, vary with wavelength. When plane-polarized light at 45° with the fast and slow directions falls on the sheet, the vibration is resolved into two equal components along the axes. As the waves progress through the sheet, one will advance in phase relative to the other, because of the difference in wavelength. The slow wave will gain in phase over the fast wave. The difference in wavelengths in a distance t will be nt/λ - n't/&lambda, where n and n' are the two indices of refraction, and λ is the vacuum wavelength. For a quarter-wave plate, this is set equal to 1/4, and the result is t = λ/4(n - n'), or t = 61λ. For sodium light, t = 0.036 mm, which is quite practical.

If the quarter-wave plate is viewed through crossed polaroids, the transmitted intensity will be zero when the fast or slow direction is in the direction of the first polaroid. This is independent of wavelength, and does not depend on the creation of circular polariztion. If the plate is rotated to the 45° position, then circular polarization is produced, and no change in intensity will be seen on rotating the second polarizer. This is also the case for unpolarized light, but circular polarization is very special. It is possible to identify whether the circular polarization is right- or left-handed, and which of the mica directions is fast and which slow, if this information is required. A second quarter-wave plate is required if the first one is used for creating the circular polarization.

Elliptical polarization can be described very simply by referring to the major and minor axes of the ellipse as the coordinate axes. Then, the light vector is given by x = A sin ωt and y = B cos ωt. A and B are the semi-axes, which can be oriented in any direction. If A and B have the same sign, it is right elliptical; if their signs are different, it is left elliptical, as in the case of circular polarization. If a quarter-wave plate is oriented with its axes parallel to those of the ellipse (this requirement is essential), then linear polarization is created with an inclination A/B with respect to the axes. Then, an analyzer will give zero intensity when its axis is perpendicular to the linear polarization, and full intensity when parallel. Elliptically polarized light is created by the inverse process.

The polarization state of light beam can be deduced with a polaroid (or Nicol prism) and a quarter-wave plate. If there is no intensity variation when the polaroid is rotated, then we have natural light or circularly-polarized light. Looking through the quarter-wave plate, if we still get no variation, then there is no circular polarization. If there is, then if the intensity can be extinguished, the light is circularly polarized. Otherwise, it is a mixture of natural and circularly-polarized light. If we do find a variation of intensity on rotating the polaroid, if the minimum is zero, then we have plane-polarized light. Using the quarter-wave plate oriented with an axis in the direction of the maximum, if we now can find a minimum of zero, we have elliptically-polarized light. If the maximum is still at the same orientation, we have partly plane-polarized light, with no elliptical component. If the maximum is at a different orientation, we have partially elliptically-polarized and partly plane-polarized light or unpolarized light.

You can demonstrate all possible paths of the tip of the light vector with the aid of an oscilloscope. Simply apply nearly equal frequencies (differing by a fraction of a herz) to the x- and y-axes, varying the amplitudes as convenient. This will give you a motion picture with a slowly varying phase difference. The path will always be an ellipse tangent to a rectangle, with the major axis along a diagonal of the rectangle. If the amplitudes are equal, the path will change from a circle to a diagonal of the square and back again. Only with a phase difference of 90° will you see the circle of circular polarization. If the phase difference is not 90°, the result will be elliptical polarization.

All the experiments on diffraction, interference, polarization and double refraction demonstrate the wonderful validity of working with an unobservable amplitude and phase to explain the observable intensity, the square of the amplitude. This is very similar to the situation in quantum mechanics.

An example of this interesting phenomenon is shown at the right. It is a good example of the propagation of light in crystals and the interference of polarized light. This pattern is for one of the simplest cases, a uniaxial crystal slab cut perpendicular to the optic axis. In this case, it is calcite, and the polarizers are crossed. Distinctive forms are produced for slabs cut parallel to the optic axis, and for biaxial crystals cut perpendicular to the bisector of the optic axes.

The setup for observing these patterns is shown at the left. Collimated monochromatic light passes through a polarizer, then through a short-focus lens, and falls on the crystal plate. The light is again rendered parallel by a second lens and passes through a second polarizer, the analyzer. The main idea is to produce a fan of rays passing through the crystal at different angles to the axis. In the pattern, a circle centred at the origin corresponds to a certain angle with the axis of the lenses, which here is the same as the optic axis of the uniaxial crystal.

Within the crystal slab, each ray is resolved into ordinary and extraordinary rays, which have different speeds of propagation. These rays are polarized at right angles in a plane normal to the ray. The plane-polarized incident light, here assumed vertical, is first resolved along the o and e axes. The analyzer then resolves these vibrations along its own axis, and the two vibrations may then interfere.

In the case of a uniaxial crystal cut perpendicular to the optic axis, the o and e directions are worked out as shown in the figure at the right. This shows a ray in a horizontal plane, making an angle φ with the optic axis. From this angle, the velocities of the ordinary and extraordinary rays can be found. The o-vibration must be normal to the horizontal plane, and the e-vibration normal to that, as shown. When the rays are bent by the lens, the result is as shown in the front. Now, everything is the same if the ray is rotated about the axis of the lenses, in particular the direction of the optic axis. Therefore, the o-direction is always tangent to the circle, while the e-direction is radial. In other cases, it is much more difficult to find the o- and e-directions; only this case is simple enough to visualize easily.

We can make several deductions from this. Rays at the 12 and 6 o'clock positions are completely o-rays, while at the 3 and 9 o'clock positions are completely e-rays, in both cases polarized vertically, the same as the polarizer. Therefore, all rays at these orientations will be extinguished by a crossed analyzer, giving a dark cross in the pattern. If you draw vector diagrams for several orientations, you will find that the interfering amplitudes E' and E" are often about the same, so fringe visibility will remain close to 1 while the intensity is reduced to zero approaching the dark cross. With a fixed angle θ, the phase difference between o and e rays will increase steadily as r increases, because of the increasing difference between the velocities away from the axis, as well as because of the greater distance d = t sec φ, where t is the thickness of the slab. Therefore, we should see a series of fringes of good visibility with decreasing spacing. If you examine the picture of the pattern presented above, these predictions will be corroborated.

At the centre of the pattern, the light travels along the optic axis, so there is no distinction between o and e waves, and the light will propagate with no alteration. From the crossed polarizer and analyzer, we expect a dark centre, which indeed appears for calcite. If the polarizer and analyzer are parallel, we may simply interchange dark and light in the pattern. Returning to crossed polarizer and analyzer, if we examine a quartz crystal in this way there is a surprising result: the centre is light, not dark. The reason for this is that quartz is optically active; that is, a plane-polarized beam along the optic axis will experience a rotation of its plane of polarization. The spot at the centre will be alternately dark and light as the thickness of the plate increases. For light of wavelength 589.3 nm, right-handed quartz rotates the plane of polarization by 21.7° per mm to the right (looking into the beam), and the rotation is a strong function of wavelength, increasing for shorter wavelength. The reason is that right and left circular polarizations travel at different speeds in quartz. Quartz crystals can be right- or left-handed, which is reflected in the external form as well as in the atomic structure. The crystals and structures are mirror images of each other.

M. Born and E. Wolf, Principles of Optics (London: Pergamon Press, 1959), Chapter 14.

F. A. Jenkins and H. E. white, Fundamentals of Optics, 2nd ed. (New York: McGraw-Hill, 1950), Chapter 25.

M. Abraham and R. Becker, The Classical Theory of Electricity and Magnetism, 2nd English edition (New York: Hafner, 1949). Includes vector fields and uses cgs units. An excellent and famous intermediate text.

M. Minnaert, The Nature of Light and Colour in the Open Air (New York: Dover, 1954).

Composed by J. B. Calvert
Created 19 July 2007
Last revised