Interference and Diffraction in Optics
This article is an extension of the article "Electromagnetic Waves in Crystals", and may reference certain topics discussed there.
- Interference and Diffraction
- Cornu's Spiral and Fresnel diffraction
- Fraunhofer Diffraction and diffraction gratings
- Lloyd's Mirror and stellar interferometry
- The Michelson Interferometer
- Other Interferometers and Interference Phenomena with interference in scattered light and Mach-Zehnder, Sagnac, Jamin, Fabry-Perot, series and speckle interferometers
- Fourier Optics
- References
Interference and Diffraction
The terms "interference" and "diffraction" were originally used with the Newtonian corpuscular theory of light, but were taken over to describe the same phenomena in the new wave theory. What is called "interference" refers to the operation of the principle of superposition: the amplitudes in two light fields simply add, but in no way affect each other or "interfere". This is a fundamental property of the Huygens-Fresnel theory of the propagation of light, and appears in every application of it. However, it may be useful to think of "interference" in a restricted sense as involving a countable number of beams (often two) with the characteristic appearance of fringes, periodic spatial variations in intensity.
"Diffraction" may refer to all the phenomena observed near shadows, or may be limited to the property of waves to bend around an obstacle. If used in this restricted sense, then the observed fringes are a result of interference of the diffracted waves with others. The apparent absence of diffraction of light was strong evidence against a wave theory. However, diffraction of light was eventually recognized (by Grimaldi, 1665) at a remarkably late date. It was also a prediction of Huygens' wavelet theory, invented to explain double refraction. However, there was no periodicity in Huygens' theory, and no explanation of fringes.
Fresnel combined the periodicity of light discovered by Young with the wavelet idea of Huygens. Each point on a wavefront at a given instant is the source of a spherical wavelet. The sum of the wavelets emitted from all points on the wavefront at an observation point P is the resultant amplitude there, and the intensity is the square of this amplitude. This Huygens-Fresnel principle, published in 1818, is remarkably in accord with observations.
There are several reasons why diffraction phenomena are so difficult to observe that they were not recognized until Grimaldi's time. These are: lack of coherence in the light source; insufficient intensity of the light source; and small size of the pattern. Coherence is the ability to produce interference fringes, demanding stable phase relations both in time and space, called temporal and spatial coherence, respectively. White light, with wavelengths between 400 and 700 nm, can produce fringes only in low orders, as in oil films or Newton's rings. Good temporal coherence demands monochromaticity. The coherence time is roughly the reciprocal of the frequency bandwidth. Spatial coherence means that the fringes will fall at definite locations, not smeared out over the observing screen, as happens with broad sources. They may indeed produce fringes, but they overlap and cannot be seen. The Sun is a bright source of nearly parallel light, but not parallel enough to make diffraction fringes distinct.
Coherence can be provided by using a spectral lamp (sodium, or mercury with a filter) and a pinhole, perhaps preceded by a condensing lens. The disadvantage, however, is a greatly reduced intensity. If the fringes to be viewed are linear, the intensity can be greatly increased by using a slit, oriented parallel to the fringes. At the present time, a laser gives bright coherent light that will exhibit fringes around any shadow. The beam has to be expanded by using a short-focus lens.
Diffraction phenomena seem to be properties of solutions of the wave equation, and do not depend on the nature of the wave. There are no polarization effects in diffraction, as there are with reflection and refraction of light. The Huygens-Fresnel theory uses a complex scalar wave function and gives good results, though we know light is an electromagnetic wave and consists of electric and magnetic vector fields. Any variation from polarization independence is a subject of great interest, and should be investigated. Diffraction does not depend on the properties of the material of the diffracting screen--whether it is conducting or nonconducting, reflecting or absorbing, metallic or nonmetallic.
There is no better demonstration of how much can be explained by the Huygens-Fresnel theory with very little calculation than the half-period division of a spherical wavefront. The wavefront is divided into zones bounded by circles marking rings each a half-wavelength farther from the point of observation P. The wavelets contributed by elements on the boundaries of a zone are 180° different in phase, and the contributions of all the wavelets make a semicircle. For each successive zone the total contribution is slightly less than that of the zone preceding, so we have a spiral converging to a point at about the centre of the semicircle from the first zone. A phasor from the origin to this point represents the intensity at P due to the entire wave. There is a difficulty here, since the sum of all the contributions lags the original wave by 90°. This is not surprising, since the contributions have to travel a greater distance. The difficulty is overcome in the Kirchhoff diffraction theory, which provides a rigorous mathematical basis for the Huygens-Fresnel theory, which shows that the wavelets must be advanced in phase by 90°. Of course this is not physical, but cannot be avoided in the theory, and merely shows that the idea of each point on a wavefront's being the source of a wavelet is naive. Useful, but naive.
Fresnel knew that the amplitude of the wavelet had to depend on its direction of emission from the wavefront, since there was no back wave. He assumed that the emission was entirely in the forward hemisphere, decreasing from a maximum along the normal to the wavefront to zero at 90° This was inaccurate, but had no effect on the predictions of the theory. Kirchhoff showed that the correct inclination factor was -(i/2λ)(1 + cos χ), where χ is the angle with respect to the normal.
One immediate prediction can be made of the intensity at a point P in the centre of the shadow of a circular obstacle. Now we begin the half-wave zones at the periphery of the obstacle, and proceed as before. The prediction is that the intensity at P is exactly what would exist in the absence of the obstacle. "Absurd!" exclaimed Poisson, who did the calculation but not the experiment. His co-adherent to the Newtonian corpuscular theory, Arago, did the experiment and saw the bright dot in the centre of the shadow. This is only the most famous of the remarkable predictions of the theory, all of which were confirmed, and which utterly destroyed the corpuscular theory.
It was noted that consecutive half-period zones practically annulled each other. What would happen if alternate zones were blacked out on a screen? Surely enough, the intensity at P was immensely increased. This zone plate acted a lot like a lens. Not a very good lens, but it could image a source S into a bright point P. Zone plates are easily made by photographing a master drawing, and printing the result on transparent plastic. This was easier to do with emulsion photography slides than with a digital camera and computer (which I have not yet tried).
Cornu's Spiral
 For treating diffraction at a straight edge, a slit or an opaque strip, it is useful to consider a cylindrical wavefront. In the figure, S is a slit source emitting a cylindrical wave of radius a. P is the observation point, which is at a distance b from the point V on the wavefront on the line joining S and P. We can choose any convenient value of a; here, V could be the upper edge of a screen that blocks off the wavefront below it. An element ds of the wavefront is assumed to emit a cylindrical wavelet, and the amplitude at P is the sum of the amplitudes of all visible wavelets at P. The wavelet emitted from V travels a distance b to P, while that from ds travels a distance b + Δ = d. Δ is the additional retardation of this wavelet with respect to the direct one from V.
For treating diffraction at a straight edge, a slit or an opaque strip, it is useful to consider a cylindrical wavefront. In the figure, S is a slit source emitting a cylindrical wave of radius a. P is the observation point, which is at a distance b from the point V on the wavefront on the line joining S and P. We can choose any convenient value of a; here, V could be the upper edge of a screen that blocks off the wavefront below it. An element ds of the wavefront is assumed to emit a cylindrical wavelet, and the amplitude at P is the sum of the amplitudes of all visible wavelets at P. The wavelet emitted from V travels a distance b to P, while that from ds travels a distance b + Δ = d. Δ is the additional retardation of this wavelet with respect to the direct one from V.
The amplitude contributed at P by the wavelet from ds will be dy = (c ds/√d) sin 2π[(t/T - b/λ) - Δ/λ], where c is a constant proportional to the amplitude of the wave from S, and the √d expresses the spreading of the cylindrical wave. The value of this amplitude will not be significant, however. Now we factor out the Δ dependence to find y = (c/√d) sin 2π(t/T - b/λ) cos 2πΔ/λ ds - (c/√d)cos 2π(t/T - b/λ) sin 2πΔ/λ ds. All we have to do now is integrate this over the visible portion of the wavefront, which we will assume extends from s = 0 to s.
Δ is, of course, a function of s, which we find by using the law of cosines in the triangle S-ds-P: (b + Δ)2 = (a + b)2 + a2 - 2a(a + b)cos φ. After a little easy algebra, we find that (b + Δ)2 = 4a(a + b)sin2(φ/2) + b2, using (1 - cos φ) =2sin2(φ/2). Now, s = aφ, so that if we assume φ small enough that the sine can be replaced by the angle, we get 2bΔ + Δ2 = (1 + b/a)s2. Neglecting Δ2 compared to bΔ, we have 2bδ = (1 + b/a)s2, or Δ = [(a + b)/2ab]s2, which is the desired relation.
The argument 2πΔ/&lambda = (π/2)[2(a + b)/λab]s2, so it is convenient to define a new variable v = √[2(a + b)/λab]s. Then, the integrals we have to evaluate are S = ∫sin (πv2/2)dv and C = ∫cos (πv2/2)dv. If we define new variables A and θ so that C = A cos θ and S = A sin θ, the expression for the amplitude at P becomes y = A sin 2π[t/T - b/λ - θ/2π). Some extra constant factors must be included in A, but its exact value is not important.
From the definitions of A and θ, we find that A2(cos2θ + sin2θ) = A2 = C2 + S2, and θ = tan-1(S/C). We can get everything we need from the integrals S and C. These are the Fresnel Integrals, which are tabulated. When corresponding values for a give v are plotted on rectangular coordinates with C horizontal and S vertical, the result is the pleasing Cornu's Spiral, displayed below. This curve is also called the clothoid, and is a good transition curve in route design, since its curvature is proportional to arc length. It is named after Marie Alfred Cornu, 1841-1902, professor at the École Polytechnique. The properties S(∞) = C(∞) = 1/2, and S(-v) = -S(v), C(-v) = -C(v), which are easily derived from the integrals, are evident from the plot.
 Since the intensity is proportional to S2 + C2, a line drawn between any two points on the spiral is the amplitude corresponding to integration between the two values of v. For example, v = 0 to v = ∞ corresponds to the entire wavefront above a straight edge screen. This is a vector from (0,0) to (1/2,1/2), of length 1/√2. The whole wavefront corresponds to the line from (-1/2,-1/2) to (1/2,1/2), of length √2. Since intensities are proportional to the squares of amplitudes, the whole wavefront gives 2, while the upper half gives 1/2, or 1/4 of the unobstructed intensity, as is observed.
Since the intensity is proportional to S2 + C2, a line drawn between any two points on the spiral is the amplitude corresponding to integration between the two values of v. For example, v = 0 to v = ∞ corresponds to the entire wavefront above a straight edge screen. This is a vector from (0,0) to (1/2,1/2), of length 1/√2. The whole wavefront corresponds to the line from (-1/2,-1/2) to (1/2,1/2), of length √2. Since intensities are proportional to the squares of amplitudes, the whole wavefront gives 2, while the upper half gives 1/2, or 1/4 of the unobstructed intensity, as is observed.
The phase of the diffracted wave with respect to the direct wave from V is given by S/V, or the slope of the amplitude line. We note that the contribution from the upper half of the wavefront is 45°, or π/4 behind the direct wave. Similarly, the contribution from the lower half of the wavefront is 225° or 5π/4 behind the direct wave. These waves are what occur just below and just above the geometrical shadow, and are the edge waves of the luminous edge. The wavefronts are not discontinuous at the shadow edge, but join smoothly, as a deeper analysis shows. That the total contribution from the whole wavefront seems to be 45° behind the direct wave is the same kind of difficulty that occurs with spherical waves, where the discrepancy is 90°. This is nothing to worry about, since it has a solution in more rigorous diffraction theory, and does not affect our deductions from Cornu's Spiral.
 A cross-section showing phase relationships at the shadow boundary is shown at the right. The fringes above the boundary can be considered as due to the interference of the unobstructed wave with the edge wave; this gives the correct distribution of intensity. Below the boundary, the intensity decreases monotonically to zero. The edge wave exists in other geometries as well. It explains the Poisson-Arago spot in the centre of the shadow of a disc, as well as the faint concentric rings surrounding it.
A cross-section showing phase relationships at the shadow boundary is shown at the right. The fringes above the boundary can be considered as due to the interference of the unobstructed wave with the edge wave; this gives the correct distribution of intensity. Below the boundary, the intensity decreases monotonically to zero. The edge wave exists in other geometries as well. It explains the Poisson-Arago spot in the centre of the shadow of a disc, as well as the faint concentric rings surrounding it.
The tangent to the spiral is given by dy/dx = (dS/dv)/(dC/dv). Since the derivatives of the integrals are just the integrands, we see that dy/dx = (π/2)v2. The first vertical tangent occurs for v = 1. For v = 2, the tangent is horizontal, and so forth. Some applications of Cornu's Spiral are given below. On the left, the contribution of the upper half of the incident wavefront is shown, with its phase relations. The contribution of the lower half is similar, except that the end of the vector is at (-1/2,-1/2), and makes the angle 5π/4 instead. As we go into the shadow, imagine the end of the vector start from the origin and move up the curve. The right-hand figure shows the effect of moving up into the illuminated region, which is equivalent to lowering the straight edge. Now the end of the vector moves down the curve, takes a maximum value, then decreases, and so on as the end of the vector spirals in to the point (-1/2,-1/2). It is not hard to find the intensity variation in the straight-edge diffraction pattern in this way, and the result agrees excellently with experiment.

It should be clear how to use Cornu's Spiral not only for a straight edge, but also for slits and opaque strips, simply by considering the pertinent parts of the wavefront. Computer programs are easily written that can plot any pattern required, using Fresnel integrals. The actual distances s at the aperture are related to the dimensionless v by v = √[2(a + b)/abλ]s. For an incident plane wave, a = ∞, and v = √(2/bλ)s. For visible light, the small scale of the phenomenon should be appreciated. Only a small part of the wavefront contributes significantly, so our approximations are valid. Another help is that the half-period strips decrease rapidly in area, unlike in the case of spherical division, so various refinements are not necessary. The fringes produced by Fresnel diffraction (of which this is an example, since the phase of the wavelets is a quadratic function of s) are not of high visibility, since they do not usually go to zero intensity. The source and observation point are a great distance from the screen, measured in wavelengths, which is a requirement of the Fresnel-Huygens theory. Good illustrations in Jenkins and White compare photographed patterns with the predictions of Cornu's Spiral. Particularly to be noted are the equally-spaced, high-visibility fringes in the shadow of an opaque strip, looking very much like two-beam interference, which they are.
Jenkins and White present the same argument used here for deriving the Fresnel integrals, but with a few bumps along the way that I hope I have clarified. Born and Wolf give a more rigorous development, with a proper integration in two directions, but it is more difficult to follow.
Fraunhofer Diffraction
If we focus diffracted light on a screen, using a lens or concave mirror, the Fraunhofer diffraction pattern appears. The screen is placed at the focal plane of the lens or mirror, so that parallel diffracted rays are brought together to interfere. The fringes are brighter and of higher visibility than Fresnel fringes, and much more useful for measurement and other purposes. For this reason, Fraunhofer diffraction is of great importance in optics. It is also easy to analyze for simple geometries--we will not even need any explicit integrals!
 Let's begin with a single slit of width a, illuminated by collimated light. At an angle θ = 0, all the wavelets from a wavefront are brought together at the focal point F, and the total amplitude may be denoted by Ro, and the intensity will be Io = Ro2. At an angle θ, wavelets from the bottom of the slit will travel an extra distance a sin θ with respect to those from the top. This corresponds to a phase difference of 2β = 2πa sin θ/&lambda. The plot of the resultant amplitude as we go from top to bottom of the slit will be a circular arc, subtending an angle of 2β, and of total length Ro. The vibration curve is a circle, because the phase difference is proportional to the length of the curve, as in s = rθ. If R is the length of the chord, the resultant amplitude for the whole slit, and r is the radius of the arc, then R = 2r sin β. However, Ro = rβ, so r can be eliminated and we find R = Ro(sin β/β) or R = Rosinc β. This is the single-slit Fraunhofer diffraction pattern. As a becomes comparable to the wavelength, the diffracted light is distributed in a broad cone. The first minimum of R occurs when the vibration arc closes into a circle, at β = π.
Let's begin with a single slit of width a, illuminated by collimated light. At an angle θ = 0, all the wavelets from a wavefront are brought together at the focal point F, and the total amplitude may be denoted by Ro, and the intensity will be Io = Ro2. At an angle θ, wavelets from the bottom of the slit will travel an extra distance a sin θ with respect to those from the top. This corresponds to a phase difference of 2β = 2πa sin θ/&lambda. The plot of the resultant amplitude as we go from top to bottom of the slit will be a circular arc, subtending an angle of 2β, and of total length Ro. The vibration curve is a circle, because the phase difference is proportional to the length of the curve, as in s = rθ. If R is the length of the chord, the resultant amplitude for the whole slit, and r is the radius of the arc, then R = 2r sin β. However, Ro = rβ, so r can be eliminated and we find R = Ro(sin β/β) or R = Rosinc β. This is the single-slit Fraunhofer diffraction pattern. As a becomes comparable to the wavelength, the diffracted light is distributed in a broad cone. The first minimum of R occurs when the vibration arc closes into a circle, at β = π.
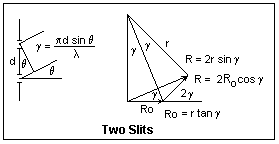 Now suppose we have two narrow slits separated by a distance d. The Fraunhofer pattern is two-beam interference, as we already know, and the fringe visibility is unity. The extra distance travelled by the light from the lower slit is d sin θ, so the phase difference is 2πd sin θ/λ = 2γ. The vibration diagram consists of two vectors of length Ro making an angle of 2γ with each other, and R is their vector sum. From the isosceles triangle thus formed, it is simple to see that R = 2Ro cos γ. We can make this more like the single-slit analysis by considering R as the third side of an isosceles triangle with equal sides r and angle 2γ. Then, R = 2r sin γ and Ro = r tan γ, from which we find the same result on eliminating r. We have not included the effect of obliquity on the amplitudes of the interfering waves. This can be done by multiplying by the factor sin β/&beta. Note that each amplitude Ro is the chord of a circular vibration arc.
Now suppose we have two narrow slits separated by a distance d. The Fraunhofer pattern is two-beam interference, as we already know, and the fringe visibility is unity. The extra distance travelled by the light from the lower slit is d sin θ, so the phase difference is 2πd sin θ/λ = 2γ. The vibration diagram consists of two vectors of length Ro making an angle of 2γ with each other, and R is their vector sum. From the isosceles triangle thus formed, it is simple to see that R = 2Ro cos γ. We can make this more like the single-slit analysis by considering R as the third side of an isosceles triangle with equal sides r and angle 2γ. Then, R = 2r sin γ and Ro = r tan γ, from which we find the same result on eliminating r. We have not included the effect of obliquity on the amplitudes of the interfering waves. This can be done by multiplying by the factor sin β/&beta. Note that each amplitude Ro is the chord of a circular vibration arc.
The condition for bright fringes is cos γ = ±1, or γ = 0, π, 2π, ..., mπ, ... . In terms of θ, this is d sin θ = mλ, which means that there is a whole number of wavelengths in the path difference. m is called the order of the fringe. Each increase of unity in the order means that the amplitude vector rotates through a full circle. This, of course, gives the same triangle (neglecting the decrease in amplitude with obliquity).
 It is not difficult now to leap to the case of a large number N of slits of spacing d. The vibration curve is a polygon that approximates the arc of a circle, and the closing side of the polygon is the desired amplitude R. The angle between each elementary vector and the next is 2γ, so the total angle subtended by R is 2Nγ. If r is the radius of the circle, then R = 2r sin Nγ, while Ro = 2r sin γ. Therefore, R = Rosin Nγ/sin γ. As γ approaches zero, R = RoNγ/γ = NRo. Therefore, the maximum intensity is Im = N2Io, where Io is the intensity due to a single slit. The same holds for γ = mπ. These are the principal maxima. The first principal maximum is at θ = 0, whatever the value of λ, but the positions of the succeeding ones depend on the wavelength. As in the case of the double slit, the maximum of order m corresponds to m wavelengths path difference between two successive slits. It is usual to multiply the expression for the amplitude by the single-slit factor sin β/β to account for the diffractive spread of the light. In most cases, the factor (sin β/β)2 in the intensity is at best a rough approximation, since the grooves are not regular slits of width a.
It is not difficult now to leap to the case of a large number N of slits of spacing d. The vibration curve is a polygon that approximates the arc of a circle, and the closing side of the polygon is the desired amplitude R. The angle between each elementary vector and the next is 2γ, so the total angle subtended by R is 2Nγ. If r is the radius of the circle, then R = 2r sin Nγ, while Ro = 2r sin γ. Therefore, R = Rosin Nγ/sin γ. As γ approaches zero, R = RoNγ/γ = NRo. Therefore, the maximum intensity is Im = N2Io, where Io is the intensity due to a single slit. The same holds for γ = mπ. These are the principal maxima. The first principal maximum is at θ = 0, whatever the value of λ, but the positions of the succeeding ones depend on the wavelength. As in the case of the double slit, the maximum of order m corresponds to m wavelengths path difference between two successive slits. It is usual to multiply the expression for the amplitude by the single-slit factor sin β/β to account for the diffractive spread of the light. In most cases, the factor (sin β/β)2 in the intensity is at best a rough approximation, since the grooves are not regular slits of width a.
This array of slits is called a diffraction grating. A typical grating for visible light has about 15,000 lines per inch, or d = 1690 nm. Now consider an angle θ such that the difference in paths at the extreme ends of the grating is one wavelength. The wavelet from one end of the grating will be 180° out of phase with the wavelet from the middle of the grating, and so they will cancel. The same thing holds for each slit as we move from the top of the middle, so we will have zero intensity. In general, since the path difference in the mth order is Nmλ, and this gives a principal maximum, the angle that gives a path difference Nmλ + λ will also give a zero. Let the breadth of the grating be b = Nd. The width of the beam will be b cos θ, so the angle δ will be given by b cos θ sin δ = λ, or sin δ = λ/(b cos θ). This is surely a very small angle, so δ = λ/(b cos θ) = λ/(Nd cos θ). That is, the principal maxima are very narrow, which makes the grating an excellent spectroscopic tool.
The relation between wavelength, angle and order is given by d sin θ = m&lambda. If the light is incident at an angle i with the normal to the grating, then we must replace sin θ by sin i + sin θ, as is clear from a diagram. Taking the derivative with respect to λ gives d cos θ dθ = m dλ. Replacing dθ by λ/(Nd cos θ), we find that λ/dλ = mN. This is the resolving power of the grating, the ratio of a wavelength to the smallest detectable wavelength difference in its vicinity. We have applied Rayleigh's criterion for resolution, when one maximum falls on the first zero of the other. The same equation gives us the angular dispersion dθ/dλ = m/(d cos θ).
Gratings are made by ruling fine grooves with a diamond point in an aluminium film deposited on a substrate, such as glass. These are, therefore, reflecting gratings. Replica gratings are made by covering the master grating with a film of collodion or plastic, and then stripping it off. These may be transmission gratings, or may be silvered to be reflecting gratings. Gratings may be ruled on a concave mirror, so that lenses are not required for collimation or observation. These are, of course, reflecting gratings. The grooves may be specially shaped to throw light into the angles that will be used. These are blazed gratings, which can give a greatly improved intensity. The ruling must be very accurate to avoid the appearance of spurious lines or ghosts. A periodic error produces the easily-recognized Rowland ghosts that symmetrically accompany a line. More complex errors may create Lyman ghosts that appear singly.
 The most common mounting (as it is called) for a plane reflecting grating is the Littrow. The slit
S and plate P or other recording medium are placed one above the other at one end. At the other, a good achromatic lens L is placed in front of the grating, which can be rotated to select the wavelength interval received on the plate. The incident and diffracted light trace the same path in opposite directions. A small transmission grating can replace the prism in a spectrometer, where the angles can be accurately measured.
The most common mounting (as it is called) for a plane reflecting grating is the Littrow. The slit
S and plate P or other recording medium are placed one above the other at one end. At the other, a good achromatic lens L is placed in front of the grating, which can be rotated to select the wavelength interval received on the plate. The incident and diffracted light trace the same path in opposite directions. A small transmission grating can replace the prism in a spectrometer, where the angles can be accurately measured.
Large concave gratings were once popular for research, and may still be useful. A typical example had a radius of 21 ft.. A point source this distance in front of the grating will produce a beam that is again focused at this point C after reflection from the mirror (the rays are radii). If we draw a circle of a diameter equal to the radius of the mirror, C is on this circle. If a source is at some other point S, b drawing rays and using the law of reflection, its beam is focused at some point P symmetrically to C. Also, diffracted rays from the concave grating will also be focused at a point on this circle. Therefore, if the slit and plate are both located on this circle, spectral lines will be focused on the plate. The circle is called the Rowland circle, after the inventor of the concave grating and an accurate ruling machine. The major disadvantage of this arrangement is that the imaging is very strongly astigmatic, since the mirror is being used off-axis.
In the Rowland mounting shown in the diagram, the grating and plate are mounted at the ends of a beam, the diameter of the Rowland circle apart. The ends of the beam move along the ways at right angles. Since the angle in a semicircle is a right angle, the slit S will also lie on the Rowland circle. The diffracted light is directed normal to the grating, while the angle of incidence can be varied. Henry Augustus Rowland (1848-1901), the first professor of physics at Johns Hopkins University, invented the concave grating, developed ruling machines, and studied the solar spectrum, among other things.
It is easy to use a grating with a student spectrometer. My spectrometer came with a well-mounted 300 lines/mm transmission grating. The collimator and telescope should first be adjusted, as when a prism is used. The grating holder can be placed on the prism table and oriented normal to the collimator axis by eye. The main adjustment that may be required is to make the grating lines parallel to the slit. If the observed spectrum is sharp, this may not be necessary. If it is, rotate the slit horizontal and then examine the spectra formed by a white light as the telescope is swung back and forth. Level the prism table until the spectra are parallel and do not rise or fall. This makes the rulings parallel to the axis of the spectroscope. Now restore the slit to vertical and adjust until the lines are sharp. My grating and holder were well-enough made that this adjustment was not required, so long as the prism table had previously been properly adjusted.
I used a low-pressure Hg discharge as a source, which gives strong blue (435.8 nm), green (546.1 nm) and yellow (577.0 and 579.1 nm) lines. Since the wavelengths are well-known, the experiment can be turned around to measure the grating spacing d. Measure the angle between the zero order and the desired line. One can also measure the wavelength difference between the yellow lines. Use the second or third order for greater accuracy.
Lloyd's Mirror
After the appearance of Fresnel's wave theory in 1818, many arrangements were devised to demonstrate interference and the production of fringes, contrasting with the previous rarity of such observations. We have already pointed out that the difficulty was only the provision of coherence through the use of slits to define the direction, and monochromaticity so the fringes would not overlap. It was found that only beams derived from the same initial beam could be made to interfere. Only recently have light sources stable enough that separate sources can interfere been available, and even then it is a difficult experiment. The reason for this, or course, is that normal light is the result of numerous individual, random, processes of emission. In a laser, these processes are made to march in step, but even the phase of a laser is not stable enough to permit interference of the beams from different lasers, in general. Beams that interfere are made by dividing a wavefront in one of two ways: one part of the wavefront can be deviated to interfere with the other part, or the amplitude of a wavefront can be divided into two parts, as when a beam is reflected and transmitted at a dielectric interface. Fringes, the result of interference, may be seen when the two beams fall on the same surface, or when two beams are brought together in the eye to create fringes on the retina.
As examples of arrangements to observe interference, we may mention Fresnel's biprism, Fresnel's mirrors, the Billet split lens, and similar devices found in the optics teaching laboratory. They all use a single slit, and create one or two virtual images of this slit, so there are two coherent sources whose overlapping beams display interference. These patterns are analyzed in the same way as in Young's Experiment, to which they are completly analogous.
 The most pleasing of these arrangments is Lloyd's Mirror, which appeared in 1834 and is illustrated at the right. The slit S is placed a short distance above the level of the mirror; reflection in the mirror produces the image slit, and the beams from these two sources interfere. One wave is direct, the other reflected in the mirror. The mirror is simply a flat piece of glass, since the reflection at glancing incidence is nearly complete, so silvering is not necessary, and would even be deleterious, since reflection at a metal surface is not as simple as reflection from a dielectric surface. The fringes are usually observed near the end of the mirror with a telescope. The mirror may be about 30-40 mm wide and 300 mm long. If a thermal light source is used, a condenser lens may be used in front of the slit to increase the intensity. A laser source must be diverged, but a slit is not then required. The reflected wave undergoes a rare-to-dense reflection, so its phase is changed by 180°, for either polarization. The fringe at the mirror surface is then a dark fringe, which can be easily seen.
The most pleasing of these arrangments is Lloyd's Mirror, which appeared in 1834 and is illustrated at the right. The slit S is placed a short distance above the level of the mirror; reflection in the mirror produces the image slit, and the beams from these two sources interfere. One wave is direct, the other reflected in the mirror. The mirror is simply a flat piece of glass, since the reflection at glancing incidence is nearly complete, so silvering is not necessary, and would even be deleterious, since reflection at a metal surface is not as simple as reflection from a dielectric surface. The fringes are usually observed near the end of the mirror with a telescope. The mirror may be about 30-40 mm wide and 300 mm long. If a thermal light source is used, a condenser lens may be used in front of the slit to increase the intensity. A laser source must be diverged, but a slit is not then required. The reflected wave undergoes a rare-to-dense reflection, so its phase is changed by 180°, for either polarization. The fringe at the mirror surface is then a dark fringe, which can be easily seen.
If white light is used, only a few coloured fringes near zero order will be seen. However, Palmer shows how to create achromatic fringes in great numbers, a very impressive demonstration. The secret is to create images of the slit in the separate colours at the correct distances from the mirror surface so that the fringes have the same spacing for all colours. They will then add to make black-and-white fringes. This is done with the aid of a Ronchi ruling as a diffraction grating. The Ronchi ruling is placed between collimator and telescope lenses (these should be good achromats, so their aberrations are well-corrected) to make a spectrum about 1 mm long. The blue will be closer to the mirror surface, the red further away. If this spectrum is located so the blue is about 1 mm from the mirror surface, and the other orders are masked off, conditions will be correct for achromatic fringes. The spacing will be small, so they should be observed with a medium-power microscope (Palmer says 100X). Very fine Ronchi rulings are now available. Palmer suggests 175 lines per inch, but I think 200 or so would be better. The size of the spectrum can be calculated from the grating equation and the focal length of the telescope lens, which should be no less than 250 mm, it seems to me.
 Let's look at the Fraunhofer pattern from two small apertures S1 and S2, as shown at the right. Each aperture alone would produce something like the Airy pattern from a disc of diameter w. This has a central bright lobe with the first minimum at an angle 1.22λ/w, where λ is the wavelength of the light used. Let P(x,y) be a typical point on a screen, with d1 and d2 the distances from P to the sources. Applying Pythagoras' Theorem, we find d22 - d12 = 2ay, where a is the distance between the sources. This shows that d2 - d1 = 2ay/(d2 + d1). If z is large compared to the other distances involved, the sum of the distances is approximately 2d, where d is the distance from the midpoint of the line joining the sources. Then we have simply Δd = ay/d = a sin θ, just as in the case of two slits. Therefore, the Airy disc is crossed by parallel fringes, that may be white light fringes. The fringes are not curved, as might be expected.
Let's look at the Fraunhofer pattern from two small apertures S1 and S2, as shown at the right. Each aperture alone would produce something like the Airy pattern from a disc of diameter w. This has a central bright lobe with the first minimum at an angle 1.22λ/w, where λ is the wavelength of the light used. Let P(x,y) be a typical point on a screen, with d1 and d2 the distances from P to the sources. Applying Pythagoras' Theorem, we find d22 - d12 = 2ay, where a is the distance between the sources. This shows that d2 - d1 = 2ay/(d2 + d1). If z is large compared to the other distances involved, the sum of the distances is approximately 2d, where d is the distance from the midpoint of the line joining the sources. Then we have simply Δd = ay/d = a sin θ, just as in the case of two slits. Therefore, the Airy disc is crossed by parallel fringes, that may be white light fringes. The fringes are not curved, as might be expected.
Consider a uniform disc source that subtends an angle θ at the observer. If we perform a double slit interference experiment at increasing slit spacings h with the light from this source, we find that the fringes first disappear at a spacing h = 1.22λ/θ, when the fringes from each source element overlap to give a uniform intensity. That is, h can be taken as the diameter of a region of coherence. A 5 μm pinhole subtends an angle of θ = 5 μrad at a distance of 1 m, so the corresponding h = 122 mm, assuming λ = 500 nm. Any double slit illuminated within this region will show fringes. Pinholes are often used in the optics laboratory to create coherent light from normal sources. The sun subtends an angle of about 1/2 degree at the observer, so here h = (1.22)(500 nm)/[0.5)(π/180)] = 0.07 mm. Double-slit experiments in sunlight do not succeed. This distance is not zero, however. The lustre of metals in sunlight may be evidence of this coherence, like the speckle pattern of a laser.
Betelgeuse, α Orionis, may be the largest visible star. It is an M-class red supergiant, and fluctuates in brightness and size. Its distance is now believed to be about 540 light-years (1 l.y. = 9.46 x 1015 m), and its diameter about 800 times larger than the Sun's (1.114 x 1012 m). Therefore, it subtends an angle of about 0.045" (1 radian = 206,265"). This is large enough to be theoretically resolved by the largest telescopes, but atmospheric turbulence probably puts it beyond the reach of terrestrial telescopes. Nevertheless, special imaging methods have recently apparently resolved surface details.
Its coherence distance h = (1.22)(500 nm)(206265)/0.045 = 2.80 m or 117 inches. When Michelson faced this problem in 1920, he put two movable mirrors on a beam that reflected their light to two fixed mirrors in the aperture of the 100-inch Mount Wilson telescope, then the largest in the world. The light was brought to a focus, and fringes of a spacing determined by the distance between the two mirrors in the aperture, but using the light sampled by the outer mirrors at a greater distance. He found that the fringes disappeared when the distance between the mirrors was 121 inches, essentially equal to what we calculated above. This was the first direct measurement of a stellar diameter. There are other methods of inferring a stellar diameter, but this was a direct measurement corroborating the other methods. Since then, the distance to Betelgeuse has been found greater than was thought in 1920 (about twice as far), so the diameter has been corrected correspondingly. Michelson's stellar interferometer should not be confused with the Michelson interferometer that is treated in the next section.
Michelson's method is ingenious, but very difficult to carry out in practice, so it was applicable only to the stars of largest angular diameter, such as Betelgeuse and Arcturus. More recently, a new method was developed by Hanbury Brown and Twiss that measured the correlation between the fluctuations in the photocurrents of two photomultipliers separated by a large distance. This electronic method was much easier to handle than the optical method of bringing the two beams together at one point to interfere. It is interpreted the same way, but the theory is more difficult and unfamiliar. Eminent physicists who did not know much about photons said it was impossible. It has allowed measurements on a much larger variety of stars.
The Michelson Interferometer
 The Michelson Interferometer, illustrated at the left, is a simple and elegant two-beam interference arrangement, apparently suggested by the requirements of the ether drift experiment first performed by Michelson and Morley in 1887, that the two light paths be at right angles. It is a "meter" because mirror M1 can be moved with an accurate screw to change the length of one of the two paths.
The Michelson Interferometer, illustrated at the left, is a simple and elegant two-beam interference arrangement, apparently suggested by the requirements of the ether drift experiment first performed by Michelson and Morley in 1887, that the two light paths be at right angles. It is a "meter" because mirror M1 can be moved with an accurate screw to change the length of one of the two paths.
Light from the monochromatic broad source S is reflected by the glass plate B, called the beamsplitter. It is actually reflected by both surfaces, which is somewhat troublesome. The back surface of B may be lightly silvered, which then makes the reflection at this surface much the stronger of the two. The reflected beam passes to mirror M1, where it is reflected again and directed toward the beamsplitter, where most of it passes through to the observer's eye E. Note that it has passed through three thicknesses of the glass at an angle of 45° with one dense-to-rare reflection. The incident light not reflected by the beamsplitter passes through glass plate C and it then reflected by fixed mirror M2. This beam again passes through C and undergoes a rare-to-dense reflection at B, from where it passes to the observer's eye E. The two beams interfere at the retina of the eye. The dotted line labelled M2' shows the position of M2 referred to the first path. When M1 is moved to coincide with M2', the two waves are 180° out of phase and give a dark fringe.
A careful procedure should be followed to align the instrument for use. Using a scale, move M1 to the same distance from the reflecting surface of the beamsplitter as M2. Check that M1 and M2 are as close to parallel as can be seen by eye. Now turn on the source, and focus your eye on M1. If you are lucky, you will see fine parallel fringes. These are just like those seen in thin films. They are arcs of circles, convex toward the side of smaller separation of the mirrors. Adjust the vertical position until the fringes are vertical. Then adjust the horizontal position, always trying to make the fringes expand, until you achieve the dark fringe that fills the mirror and shows that the mirrors are parallel. Usually M1 is fixed, and there are two tilt adjustment screws on M2, one for each degree of freedom. You can change the adjustment so that the space between the mirrors is slightly wedge-shaped, and watch the fringes move as you slowly move M1. These fringes can only be seen when the virtual separation of the mirrors is small, because at larger distances the pupil of the eye cannot receive both beams, because they have become too widely separated.
When you have the mirrors as parallel as possible, moving them apart then should show you circular fringes, looking like Newton's Rings or a Fresnel zone plate. As you move M1, fringes appear or disappear at the centre of the pattern and move outward or inward as the motion continues. The eye should be focused at infinity for these fringes. They can be seen at large separations, but become very fine. As you count fringes appearing or disappearing at the centre, you are in effect counting half-wavelengths of motion of M1. This is the basis for the use of the interferometer for measuring distances in terms of wavelengths.
The white-light source allows you to identify the zero-order fringe, when the distance between the mirrors is zero. This is best done with the parallel localized fringes. This may take a bit of work, but the zero-order will be quite evident. This fact is often of use in practical work. The purpose of the compensating plate C is to equalize the paths in glass, so the zero order can easily be found. Without C, it is impossible to find a zero-order fringe, for various reasons, among them the dispersion of the glass.
Other Interferometers and Interference Phenomena
One easy way to see fringes was even mentioned in Newton's Opticks. To repeat the observation, I used a common back-silvered mirror 50 x 100 mm and 4 mm thick. It was well-dusted with Johnson's baby powder, then shaken off. A disc with a hole in the centre made with a one-hole paper punch was placed behind the cover glass in a flashlight. The dusty mirror was propped up and viewed from about 3 m, holding the flashlight at the side of my head at the level of my eyes. When the reflection of the flashlight showed in the mirror, the mirror was seen to be crossed by parallel dark and light fringes that were clearly zero-order white light fringes. The fringes were very distinct and easy to see.
This is interference in scattered light. Light from the approximate point source is scattered by the powder, then reflected in the mirror, and also is reflected in the mirror and then scattered by the powder. Imagine one powder speck engaged in forming both beams, then all the powder specks working together. This differs from the usual thin-film interference in that at normal incidence the phase difference is zero, explaining the white-light fringes.
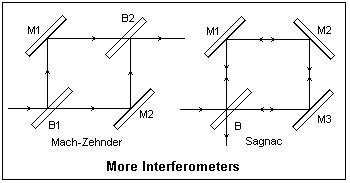 Two interesting interferometer arrangements are illustrated at the right. The two paths in the Mach-Zehnder are not only well-separated, but are also traversed in one direction only, so it is easy to compare conditions along one path with the other. For example, one beam can pass through a wind tunnel and be compared with an unmodified beam to detect density differences. This should be distinguished from schlieren methods that depend on refraction by the density differences and not interference. These will be described later. The Mach-Zehnder is very difficult to adjust, and must be very carefully put together. The two paths must agree to lengths comparable to wavelengths of light. The second beamsplitter B2 is really a beam combiner. Depending on the application, an extended or a point source may be used. Note that rotating beamsplitter B1 lengthens one path and shortens the other.
Two interesting interferometer arrangements are illustrated at the right. The two paths in the Mach-Zehnder are not only well-separated, but are also traversed in one direction only, so it is easy to compare conditions along one path with the other. For example, one beam can pass through a wind tunnel and be compared with an unmodified beam to detect density differences. This should be distinguished from schlieren methods that depend on refraction by the density differences and not interference. These will be described later. The Mach-Zehnder is very difficult to adjust, and must be very carefully put together. The two paths must agree to lengths comparable to wavelengths of light. The second beamsplitter B2 is really a beam combiner. Depending on the application, an extended or a point source may be used. Note that rotating beamsplitter B1 lengthens one path and shortens the other.
The Sagnac interferometer, invented in 1911, goes to the opposite extreme: the two paths are coincident, and are only described in opposite directions. The figure shows three mirrors for comparison with the Mach-Zehnder, but normally the Sagnac is made with only two mirrors, so the light path is triangular. The Sagnac is very easy to adjust. Palmer describes how one can be constructed on a plywood square, using optical components of normal quality.
The two paths can be affected in different ways by rotating the interferometer. Although a relativistic analysis is appropriate here, a classical analysis gives the same result, since it is a first-order effect. Rotation lengthens one path while it shortens the other, causing a phase difference that is observed as a fringe shift. The shift is ΔN = 4Aω/cλ (c is the velocity of light), where A is the area of the interferometer paths. Michelson and Gale used this method to find the angular velocity of the earth in 1925. Sagnac interferometers are used in gyroscopes for detecting angular velocities. For an area of 1 m2, an angular velocity of 120 rpm causes a shift of about 0.28 fringes in sodium D light. A ring laser inserts an optical gain mechanism in the path. The difference in frequency of the light in the two directions is proportional to ω.
 A form of the Sagnac interferometer is shown at the right, where it is called a triangle interferometer. Another name is cyclic interferometer. The light paths are like a 45-degree triangle, while the Sagnac interferometer is usually an equilateral triangle. There will be very little difference in the functioning. The source S may be a diffuse (broad) source, or a point or collimated source. The fringes are viewed at E. When the interferometer is in perfect adjustment, the light paths are symmetrical, and the clockwise and anticlockwise paths are equal in length, whatever the angle at which the light enters, as shown. This explains why the instrument is so easy to align. The mirrors do not have to be moved, only rotated. When the main images of the source are made to coincide, the instrument will be close enough to adjustment that white-light fringes can be seen at once. In the Michelson interferometer, not only must the mirrors be parallel, but also must be at the correct distances for path equality. Monochromatic light is necessary for the alignment procedure in this case.
A form of the Sagnac interferometer is shown at the right, where it is called a triangle interferometer. Another name is cyclic interferometer. The light paths are like a 45-degree triangle, while the Sagnac interferometer is usually an equilateral triangle. There will be very little difference in the functioning. The source S may be a diffuse (broad) source, or a point or collimated source. The fringes are viewed at E. When the interferometer is in perfect adjustment, the light paths are symmetrical, and the clockwise and anticlockwise paths are equal in length, whatever the angle at which the light enters, as shown. This explains why the instrument is so easy to align. The mirrors do not have to be moved, only rotated. When the main images of the source are made to coincide, the instrument will be close enough to adjustment that white-light fringes can be seen at once. In the Michelson interferometer, not only must the mirrors be parallel, but also must be at the correct distances for path equality. Monochromatic light is necessary for the alignment procedure in this case.
When one mirror is rotated slightly, as shown at the right of the figure, the clockwise and anticlockwise paths become asymmetrical and different. Although they exit parallel, the wave front is sheared and one path is slightly longer than the other, so that fringes will be observed.
Palmer describes how to build and align a triangle interferometer. Anything like this with any other form of interferometer would almost certainly be unsuccessful. As a curiosity, an inclined glass plate about 1/2" thick does affect the clockwise and anticlockwise paths differently, due to its dispersion, so the fringes can be rendered achromatic.
The Twyman-Green interferometer is a Michelson interferometer used with a collimated (or point) source of light. Lasers have greatly increased the available illumination, and are generally used today. The Twyman-Green is used for inspecting optical components; it essentially compares two nearly-plane wavefronts, one from a plane mirror and the other from the optical component under test. Points in the interference pattern correspond to points on the component, so corrections can be suggested. If a lens is being tested, a convex mirror is used to autocollimate the light passing through it, for example. Plane surfaces can be directly compared. The fringes are the usual two-beam cos2 type.
 The Jamin refractometer is illustrated at the left. It is a two-beam interferometer specially for measuring the index of refraction of a gas. The gas is introduced into T1 or T2, while the compensator C is rotated to keep the zero-order white light fringes seen through the telescope at E in the same location. C is calibrated in index of refraction. It consists of glass plates in each beam, inclined in different directions. There are several interesting features of this interferometer.
The Jamin refractometer is illustrated at the left. It is a two-beam interferometer specially for measuring the index of refraction of a gas. The gas is introduced into T1 or T2, while the compensator C is rotated to keep the zero-order white light fringes seen through the telescope at E in the same location. C is calibrated in index of refraction. It consists of glass plates in each beam, inclined in different directions. There are several interesting features of this interferometer.
The thick glass plate P1 creates a copy of the wavefront moved sideways a certain amount: the wavefront is sheared, so this is an example of a wavefront-shearing interferometer. This is actually a type of amplitude division, of course. The similar plate P2 recombines the beams. Since the path lengths are equal, we see white light fringes. These are Brewster's Fringes, white light fringes seen in a stack of thick plates. White light fringes cannot be seen in thick plates because of the large path difference. The amplitude is divided at the lower surface of the upper plate for one beam, which is reflected at the upper surface and then goes forward. The other beam undergoes a similar double reflection in the lower plate, so that the path lengths are equal. There are other paths, of course, but they are much less intense.
The Fabry-Perot interferometer, or étalon is a very simple device that can be used to study very small wavelength differences in spectroscopy. It is a film of air of thickness d between two partially-silvered plates. Spacers are used between the plates to establish the distance d, and they must be very carefully made to ensure that the plates are parallel. Fine adjustments are made by compressing them slightly with adjusting screws. The instrument is used in transmission, with wide-angle illumination. The fringe location is governed by the usual thin-film equation 2nd cos θ = mλ, where d = 1. This equation is derived in the article on crystal optics, under Mica, and it is shown there that to a good approximation θ = a√N, where a = √(λ/d). These are called Haidinger fringes, and may be said to be located "at infinity" since they are seen at the focal point of a lens. They are distinguished from Fizeau fringes, or localized fringes, such as Newton's Rings. White light fringes are, of course, not possible in this case because the order is always large. The etalon is properly adjusted when the rings do not change in radius as the eye is moved to any point.
The wavelength λ makes a ring at an angle θ in the mth order, where 2d cos θ = mλ, and a ring at an angle &theta:' in the (m - 1)st order, where 2d cos θ' = (m - 1)λ. A slightly smaller wavelength λ - Δλ coincides with the larger ring if 2d cosθ' = m(λ - Δλ). Subtracting the last two equations gives λ = mΔλ, and replacing m by its value from the first equation gives Δλ = λ2/2d cos θ, or very closely Δλ = λ2/2d. Wavelengths in this interval near λ will make rings in this interval, allowing them to be resolved. The image of a slit usually falls on the etalon, so instead of rings a vertical bar with transverse lines is seen near each spectral line. Careful measurements of the positions of these lines allows the wavelengths to be determined.
Instead of the wavelength λ, spectroscopists generally use the wave number σ = 1/λ in cm-1. Since Δσ = -Δλ/λ2, the spectral range between two rings is just Δσ = 1/2d. For d = 1 cm (a typical value), Δσ = 0.5 cm-1. For comparison, the sodium D lines are at about 16,969 cm-1, and their separation is 17.2 cm-1. The Fabry-Perot etalon is used for studying hyperfine structure.
An unusual interferometer makes use of Brewster's fringes. These were originally the white-light fringes seen in two thick plates in series. White-light fringes cannot be seen in a single plate, because of the very high order m = 2d/λ at normal incidence. However, if two plates are traversed one after the other, the reflections make paths possible with nearly zero path differences. For example, suppose one ray is reflected twice in the first plate and passes straight through the second one, while another ray passes straight through the first plate and is reflected twice in the second plate. Such rays will interfere to produce white-light fringes. Slightly inclining the plates can favor certain paths.
The series interferometer, as it is called in the Scientific American reprint book noted in the References, consists of a series of three mirrors, which are lightly-silvered plates to emphasize one reflecting surface on each plate. The light path is divided into two parts between pairs of mirrors, and these parts act like the thick plates in viewing Brewster fringes. The light paths used in the interferometer are coincident, as in the Sagnac interferometer, but one traverses the first interval three times while the other traverses the second interval three times. Therefore, a medium placed in the first interval will affect one path more than the other, and interference will be observed. The medium may be a gas whose density differences produced by local heating will produce fringes from which the density or temperature may be determined. This interferometer is not difficult to align. The mirrors must be inclined to favor the desired paths. It is used with a collimated monochromatic source, and the fringes can be projected or photographed.
When laser light is received by a matte surface, it is scattered by the irregularities of various heights, each of which becomes a coherent source with phase dependent on the height. The light from these sources interferes with the original beam to produce a seemingly random distribution of intensity, called laser speckle. The speckle is characteristic of the matte surface and is small near the surface, larger at greater distances. The speckle can be focused at any point. The eye may regard it as variously localized, even virtually behind the surface. The speckle pattern moves with the surface, and this is the basis of what is called speckle interferometry.
A method of using speckle interferometry to measure the displacement of an object is to make a double exposure of the speckle pattern, one exposure before, and the other after, the movement. The double exposure gives a pattern in which the spatial frequency corresponding to the displacement is strong. For any vicinity at x, there is a similar vicinity at x + dx, where dx is the displacement, constant at every point. If the negative is illuminated with collimated light, then in the focal plane of a lens the spatial Fourier transform of the image is produced, and the displacement will appear as parallel fringes.
In U.S. engineering practice, surface roughness was expressed in microinches. One ten-thousandth of an inch, 0.0001" is 100 μin. This is the roughness of a normal well-machined surface. Since a typical visible wavelength is about 13 μin, this corresponds to about 8 wavelengths. Such a distance is even larger than the coherence length of a monochromatic beam from a discharge lamp, so speckle is not observed with such a coherent source. When the roughness of a surface is about 10 μin, on the other hand, there is specular reflection and again speckle is not observed.
Fourier Optics
Fourier Optics refers to the use of the Fourier transform and related subjects in Optics, as applied both to the light signal itself and to the images formed by optical systems. There are three principal applications: first, Fraunhofer diffraction is equivalent to a spatial Fourier transform; second, the power spectrum is the Fourier transform of the autocorrelation function (Wiener-Khintchine Theorem); and third, an optical system can be considered to be a linear system specified by transfer functions relating the output to the input.
For functions depending on time, the Fourier transform relates the time (t) and frequency (f) domains. For functions depending on space, it relates the space (x) and spatial frequency (p) domains, in two and three as well as in one dimension. These are often called the direct and reciprocal spaces. It is a generalization of the expression of a periodic signal in terms of sinusoidal and cosinusoidal functions that are multiples of the fundamental frequency, the Fourier series, which should be familiar to the reader. Now, however, the frequency spectrum is continuous, not discrete, in general.
The fundamental integral is f(t) = ∫∫f(t')exp[2πif(t - t')]dfdt'. The letter f is used both for the frequency and for the function, and should not be confused. The limits on the integrals are +∞ to -∞ (unless otherwise explicitly specified). The first thing to be noted is that the integral over f gives the Dirac delta function δ(f - f'), since the subsequent integral over f' replaces t' by t, through the familiar property of the delta function: f(t) = ∫f(t')δ(t - t')dt'. This means that δ(t - t') = ∫exp[2πif(t - t')]df, a useful representation of the delta function.
The fundamental integral can be expressed as a two-stage process. First, we write F(f) = ∫f(t)exp(2πift)dt, and identify F(f) as the Fourier transform of f(t). Note that the product ft appearing in the integral is dimensionless: if t is in seconds, f is in 1/seconds, or Hz. If the function is f(x), then F(p) is its spatial Fourier transform. Again, xp is dimensionless, so if x is in m, the spatial frequency p is in m-1. If convenient, we use the upper-case letter for the transform and the lower-case for the direct function. We may also write F{g(t)} = G(f) to express that the Fourier transform of g(t) is G(f). The exponential transform defined here is usually the only one that we shall need. Then, the second stage is f(t) = ∫F(f)exp(-2πift)df, which is the inverse transform expressing f(t) in terms of its frequency components. Note that the sign of the exponent is negative here. I prefer to include the factor 2π in the exponents, not in front of the integral, which happens if the integration is over ω = 2πf instead of f. This eliminates factors of 2π that appear randomly here and there and really are not at all significant (but must not be got wrong!).
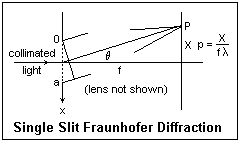 Let us now relate the Fourier transform to Fraunhofer diffraction, by considering the simple case of a single slit of width a, coherently illuminated. In the figure, x is measured positive downward from the top of the slit. Light diffracted in the direction θ is brought to a focus at the point P on a screen at the focal plane of a lens close to the aperture (this lens is not shown). The phase of the light diffracted from dx at a distance x relative to that at the top of the slit is 2πx sin θ/&lambda. Summing the contributions at point P, we get a resultant amplitude A = ∫(0,a)dx exp(2πix sin θ/λ, or A = ∫(0,a)dx exp(2πipx), where the spatial frequency p = sin θ/λ = X/fλ, to a good approximation. We have neglected the usual factors before the integral that do not affect the relative intensities. If we define the aperture function a(x) to be unity for x from 0 to a, and zero elsewhere, then the amplitude is A(p) = ∫a(x)exp(2πipx), just the Fourier transform of a(x). This is the desired result.
Let us now relate the Fourier transform to Fraunhofer diffraction, by considering the simple case of a single slit of width a, coherently illuminated. In the figure, x is measured positive downward from the top of the slit. Light diffracted in the direction θ is brought to a focus at the point P on a screen at the focal plane of a lens close to the aperture (this lens is not shown). The phase of the light diffracted from dx at a distance x relative to that at the top of the slit is 2πx sin θ/&lambda. Summing the contributions at point P, we get a resultant amplitude A = ∫(0,a)dx exp(2πix sin θ/λ, or A = ∫(0,a)dx exp(2πipx), where the spatial frequency p = sin θ/λ = X/fλ, to a good approximation. We have neglected the usual factors before the integral that do not affect the relative intensities. If we define the aperture function a(x) to be unity for x from 0 to a, and zero elsewhere, then the amplitude is A(p) = ∫a(x)exp(2πipx), just the Fourier transform of a(x). This is the desired result.
We can easily evaluate the integral, obtaining A(p) = [exp(2πipa) - 1]/2πip. This can be written A(p) = a exp(πipa)[sin(πpa)/πpa]. The phase factor is just the phase of the wave from the centre of the slit relative to the wave from the top of the slit, and does not affect the intensity. Therefore, the single-slit pattern can be expressed as the square of the amplitude a sinc(πpa), as we well know. [sinc x = sin x/x] The zeros of this function occur at πpa = mπ, so the first zero is at pa = 1, or p = 1/a, clearly showing the inverse dependence of the width of the interference pattern on the width of the slit.
From the definition of the transform, it is easy to show that if f(-x) = f(x), that is, if the diffracting aperture is symmetric about the origin, then F(-p) = F(p) as well, so that the Fraunhofer diffraction pattern is also symmetrical about the origin in the reciprocal space.
 In two dimensions, F(p,q) = ∫∫f(x,y)exp[2πi(px + qy)]dx dy. The diffraction pattern of the rectangular aperture is easily found, depending on the two spatial frequencies p = X/fλ and q = Y/fλ, where (X,Y) is a point on the screen. A more interesting problem is a circular aperture, where f(x,y) = 1 for r≤a, 0 otherwise. Using polar coordinates, we have x = r cos θ, y = r sin θ, p = k cos α and q = k sin α. k is a radial spatial frequency. When these expressions are substituted in the transform integral, we have F(k,α) = ∫(0,a)∫(0,2π)exp[2πkr cos(θ - α)]rdrdθ. From the circular symmetry, we see that F will be independent of α, so we might as well choose α = 0. The theta integral can be found in integral tables. In fact, ∫(0,2π)exp[2πikrcos(theta;)] = 2πJ0(2πkr). Now F(k,α) = 2π∫(0,a) rJ0(2πkr)dr, which also is easy to do from tables. The result is, finall, F(k,α) = 2πa2 [J1(2πka)/2πka]. The square of this is the intensity, which, of course, is the familiar Airy disc, which is illustrated above. The zeros of J1(z) are at z = 3.83171, 7.01559, 10.17347, ... . The first zero is for 2πkr = 3.83171, or k = 1.2196/d, where d = 2a, the diameter of the aperture, which is comparable to the width of the single slit. The circular aperture of diameter d is a bit narrower than a slit of width d, so its diffraction pattern is a bit wider, 1.22 appearing instead of 1.00.
In two dimensions, F(p,q) = ∫∫f(x,y)exp[2πi(px + qy)]dx dy. The diffraction pattern of the rectangular aperture is easily found, depending on the two spatial frequencies p = X/fλ and q = Y/fλ, where (X,Y) is a point on the screen. A more interesting problem is a circular aperture, where f(x,y) = 1 for r≤a, 0 otherwise. Using polar coordinates, we have x = r cos θ, y = r sin θ, p = k cos α and q = k sin α. k is a radial spatial frequency. When these expressions are substituted in the transform integral, we have F(k,α) = ∫(0,a)∫(0,2π)exp[2πkr cos(θ - α)]rdrdθ. From the circular symmetry, we see that F will be independent of α, so we might as well choose α = 0. The theta integral can be found in integral tables. In fact, ∫(0,2π)exp[2πikrcos(theta;)] = 2πJ0(2πkr). Now F(k,α) = 2π∫(0,a) rJ0(2πkr)dr, which also is easy to do from tables. The result is, finall, F(k,α) = 2πa2 [J1(2πka)/2πka]. The square of this is the intensity, which, of course, is the familiar Airy disc, which is illustrated above. The zeros of J1(z) are at z = 3.83171, 7.01559, 10.17347, ... . The first zero is for 2πkr = 3.83171, or k = 1.2196/d, where d = 2a, the diameter of the aperture, which is comparable to the width of the single slit. The circular aperture of diameter d is a bit narrower than a slit of width d, so its diffraction pattern is a bit wider, 1.22 appearing instead of 1.00.
We now motivate the discussion of convolution by considering a system that, if it produces an output y(t) when an input x(t) is applied and an output Y(t) when an input X(t) is applied, then an output ay(t) + bY(t) is produced when an input ax(t) + bX(t) is applied. This is a linear system. Some less important properties are that if x(t) = 0 for a sufficient length of time, then y(t) = 0 (stability), and for systems whose variable is time, an effect cannot precede the cause (causality).
Suppose that when we apply an impulse x(t) = δ(t) to a system, we produce a response h(t). We cannot actually apply a delta function input, but we may consider it as a limit, or simply assume that if we could apply an ideal impulse we would receive h(t). Stability demands that ∫|h(t)|dt < ∞, and causality that h(t) = 0 for t < 0. For a system that does not depend on time, of course, causality is not required. An arbitrary input x(t) can be considered as a continuous sequence of impulses, and we may find the output by adding the responses.
 In the figure, h(x) is shown as a sudden rise followed by a gradual decline to zero. This is not an unusual case. Since the area under the curve is finite, stability is satisfied. Causality is also clearly satisfied; there is no response before the impulse is applied at x = 0. In the middle diagram, the input f(τ) produces an output at x equal to the value of f(τ) times the value of the impulse response function at x. The inputs for other values of τ will have their appropriate contributions. Clearly, we need to consider values of f(τ) only for a limited range of τ, and, of course, none after τ = x. It should be easy to see that we get the same contribution from f(τ) by putting the origin of h(x) at x and reflecting it; the same value now falls under f(τ) as previously was at x, and all we need to do is multiply them to get the contribution of f(τ) to the output. The contribution from all values of f(τ) is then the integral of the product of these two functions. In fact, y(x) = ∫f(τ)h(x - τ)dτ. This is the convolution of f(x) and h(x), which we shall write g(x) = f(x)*h(x). The proper symbol is an X in a circle, but browsers do not support this.
In the figure, h(x) is shown as a sudden rise followed by a gradual decline to zero. This is not an unusual case. Since the area under the curve is finite, stability is satisfied. Causality is also clearly satisfied; there is no response before the impulse is applied at x = 0. In the middle diagram, the input f(τ) produces an output at x equal to the value of f(τ) times the value of the impulse response function at x. The inputs for other values of τ will have their appropriate contributions. Clearly, we need to consider values of f(τ) only for a limited range of τ, and, of course, none after τ = x. It should be easy to see that we get the same contribution from f(τ) by putting the origin of h(x) at x and reflecting it; the same value now falls under f(τ) as previously was at x, and all we need to do is multiply them to get the contribution of f(τ) to the output. The contribution from all values of f(τ) is then the integral of the product of these two functions. In fact, y(x) = ∫f(τ)h(x - τ)dτ. This is the convolution of f(x) and h(x), which we shall write g(x) = f(x)*h(x). The proper symbol is an X in a circle, but browsers do not support this.
It is easy to believe, and not hard to prove, that convolution is commutative: f*g = g*f. Also, f(x)*δ(x - a) = f(x - a). that is, convolution with δ(x - a) translates f(x) to the right by a. Convolution also has an astounding property: the Fourier transform of the convolution is the ordinary product of the Fourier transforms of the factors! That is, F{f(x)*g(x)} = F(p)G(p). This can be proved directly by taking the transform, but I won't do so at this time, since it will only exercise algebra and not show anything important.
Consider g(x) = δ(x - b/2) + δ(x + b/2), which represents two equal impulses a distance b apart. The transform integral is easily evaluated, using the delta functions, and the result is G(p) = exp(πib) + exp(-πipb) = 2 cos(πpb). If f(x) is the aperture function for a slit of width a, we have already found F(p) = a sinc(πpa). The convolution f(x)*g(x) represents two slits of width a whose centre are separated by a distance b. The Fourier transform of this function will be the Fraunhofer diffraction pattern of two slits. But we know that this transform is just the product of the two transforms we have just quoted. The result is 2a sinc(πpa) cos(πpb), and the square of this is the intensity. It is just what we previously found for two slits.
This is a special case of the array theorem, which states that the Fraunhofer pattern of an array of indentical apertures is the product of the transform of the aperture function and the transform of an array of point sources at the locations of the identical apertures. This array is a sum of delta functions, just as in the preceding paragraph.
 As another example, consider the convolution of a slit with itself, as shown in the figure at the right. This is easily worked out by inspection, since the slit is symmetrical about its centre, and the area of overlap is proportional to displacment. The convolution is seen to be a triangular function of twice the width of the slit. The Fourier transform of this triangular function is the square of the transform of the slit, or sinc2(πpa). This function has its zeros in the same location as for the single slit, but the side lobes are considerably less because of the squaring. If this is to be a diffraction pattern, we will need a slit of width 4a, but with amplitude attenuation varying linearly. In terms of the zeros, it is no wider than the single slit, however. This is an example of apodization, but not a particularly good one, since the side lobes are still there, if reduced in height.
As another example, consider the convolution of a slit with itself, as shown in the figure at the right. This is easily worked out by inspection, since the slit is symmetrical about its centre, and the area of overlap is proportional to displacment. The convolution is seen to be a triangular function of twice the width of the slit. The Fourier transform of this triangular function is the square of the transform of the slit, or sinc2(πpa). This function has its zeros in the same location as for the single slit, but the side lobes are considerably less because of the squaring. If this is to be a diffraction pattern, we will need a slit of width 4a, but with amplitude attenuation varying linearly. In terms of the zeros, it is no wider than the single slit, however. This is an example of apodization, but not a particularly good one, since the side lobes are still there, if reduced in height.
The Gaussian function g(x) = exp(-ax2) has a special property with respect to the Fourier transform. The transform is G(p) = ∫exp(-ax2 + 2πipx)dx = ∫exp[(√ax -πip/√a)2 +(πp)2/a]dx, where we have "completed the square". Since ∫exp(-ax2)dx = √(π/a), G(p) = √(π/a)exp(-π2p2/a). The limits on all these integrals are -∞ to +∞, as usual. The transform of the Gaussian is another Gaussian, which is the remarkable result.
From the integral we just used, the function √(a/π)exp(-ax2) is normalized; that is, its integral from -∞ to +∞ is 1, which is convenient in statistics, where the Gaussian is the Normal distribution. The average of x2 over this distribution is called the variance σ2. This is easy to calculate, since the integral is found in tables. σ2 = √(a/π)∫x2exp(-ax2)dx = 1/2a. The Gaussian is often written g(x) = exp(-x2/2σ2)/σ√(2π)], which is normalized and σ appears explicitly (it is called the standard deviation in statistics).
Our result shows that the standard deviation of the transform G(p) is σ' = 1/2πσ. If a Gaussian is wide, its transform is narrow, and vice versa. If we had an aperture with a Gaussian transmission, then the Fraunhofer diffraction pattern would be another Gaussian. Neither would show any zeros or side lobes, as we found for sharp-edged apertures. This is excellent apodization, since the side lobes are completely removed. Laser beams typically have a Gaussian profile.
The autocorrelation of a function f(t) is the function c(τ) = ∫f(t)f*(t + τ)dt of the delay τ. In case f(t) is not square integrable, we may use C(τ) = lim(T→∞) ∫(-T, T) f(t)f*(t + τ)dt. This is often the case with time functions, but not with space functions, where the first definition is satisfactory. When τ = 0, we have c(0) = ∫|f(t)|2dt, which is proportional to the total energy in the signal, often just called the total energy. If we use the second definition, this is the average power, energy per unit time, in the signal. What happens for increasing τ depends on the nature of the signal. If it is a random or noise signal, then c(τ) decreases for increasing τ.
Let's consider a determinate, non-noise, signal f(t) = A sin(ωt + ε), a typical sinusoid. We must use the second definition, since this signal is not square integrable. The integrand is A2[sin2(ωt + ε)cos(ωτ) + sin(ωt + ε)cos(ωt + ε)sin(ωτ)]. The only part surviving as T→∞ comes from the sin squared, which integrates to 1/2. The autocorrelation is then C(τ) = (A2/2)cos(ωt). This does not go to zero as τ becomes large, but oscillates with angular frequency ω. Note that the Fourier transform of the cosine consists of two delta functions at ±f. This is the frequency spectrum of the original signal. However, phase information (ε) has been lost. This is a general result: the Fourier transform of the autocorrelation is the power spectrum. This can be shown explicitly by taking the transform, and is called the Wiener-Khintchine Theorem. This is a practical method of spectroscopy and of time-series analysis.
In the Michelson interferometer, the beam reflected at the moving mirror is time-delayed or -advanced relative to the beam reflected at the fixed mirror. The delay is τ = 2cΔx, proportional to the displacement of the moving mirror. The amplitude of the superimposed beams at a square-law detector is f(t) + f(t + τ), so the signal is f(t)f*(t) + f(t + τ)f*(t + τ) + f(t)f*(t + τ). The final term is the autocorrelation; the others act like constants when the Fourier transform is taken, so the result is the signal power spectrum. The FFT algorithm makes taking the transform much easier.
One sort of noise has a wide fequency spectrum that is about constant; that is, equal frequency intervals contain equal signal energy. This is called white noise. Since the power spectrum is the Fourier transform of the autocorrelation, the autocorrelation must be a narrow peak near τ = 0. Narrow-band noise, on the other hand, gives an autocorrelation that is still large for a certain range of frequencies.
Cross-correlation is similarly defined, except that it involves two different functions f(t) and h(t). There is nothing special about τ = 0, and the cross-correlation may be small for all values of τ. If one of the functions is even, f(-t) = f(t) for example, the cross-correlation is the same as the convolution of the two functions. The Fourier transform of the cross-correlation is then the cross power spectrum of the two signals. The coherence of the light at two points can be expressed as the cross-correlation of the amplitudes at the two points.
A Ronchi ruling is an array of equal opaque and transparent strips on a transparent substrate that has many uses in optics. It may be a test object, a coarse diffraction grating, or may make the dots in a halftone illustration. The spatial Fourier transform of the ruling is a Fourer series, consisting of sinusoidal components whose frequencies are integer multiples of the fundamental frequency of the grating. Let us take for convenience the fundamental interval of (-π, π). Then a function of period 2π can be expressed as f(x) = a0/2 + a1cos x + a2cos 2x + ... + b1sin x + b2sin 2x + ... . Using the orthogonality of the sines and cosines, the constants are easily found to be an = (1/π)∫(-π,π)f(x)cos nx dx and bn = (1/π)∫(-π,π)f(x)sin nx dx. a0/2 is just the average value of f(x) in the fundamental interval. Periodicity over an infinite interval narrows the Fourier transform to a delta function at the corresponding frequency in time or space.
 If we choose the fundamental interval as shown, f(x) is an even function and only the cosine terms will survive. The integrals are easy to evaluate. The even harmonics vanish, while the odd harmonics remain, with amplitudes proportional to the reciprocals of odd integers and alternating signs. The powers in each harmonic are proportional to the squares of the amplitudes. Loss of the higher harmonics corresponds to rounding of the waveform. Note that the series converges to the function everwhere except at the jump discontinuities, where it converges to 1/2, the average of the limits as these points are approached from two sides. All of this is characteristic of Fourier series. The series is easily modified for an arbitrary fundmental interval and height. The term "square wave" refers to the equality of the lengths of 1 and 0 values, and the vertical discontinuities, not to the shape of the wave in a diagram.
If we choose the fundamental interval as shown, f(x) is an even function and only the cosine terms will survive. The integrals are easy to evaluate. The even harmonics vanish, while the odd harmonics remain, with amplitudes proportional to the reciprocals of odd integers and alternating signs. The powers in each harmonic are proportional to the squares of the amplitudes. Loss of the higher harmonics corresponds to rounding of the waveform. Note that the series converges to the function everwhere except at the jump discontinuities, where it converges to 1/2, the average of the limits as these points are approached from two sides. All of this is characteristic of Fourier series. The series is easily modified for an arbitrary fundmental interval and height. The term "square wave" refers to the equality of the lengths of 1 and 0 values, and the vertical discontinuities, not to the shape of the wave in a diagram.
 One very interesting application of Fourier optics is to spatial filtering. The setup is shown in the figure. The transform lens Lt and the imaging lens Li are well-corrected achromats, here assumed to have the same focal length f. The illumination is collimated monochromatic light. When this was provided by a pinhole and collimator, it was very difficult to get sufficient intensity. Laser sources overcome this problem very well. The lenses are located a distance 2f apart. The object, a transparency, is placed a distance f in front of Lt. An inverted image of this object is formed in the focal plane of Li. The spatial Fourier transform of the object is formed in the transform plane in the focal plane of Lt. So far as forming the transform is concerned, the object can be at any location in front of Lt, since the illumination is parallel. The only difficulty is that the farther it is from Lt, the smaller is the angular aperture for the diffracted rays to enter Lt. We locate it so that Li inverts the transform in its focal plane, where the image is formed. By the use of a mask in the transform plane, we may block out any undesired spatial frequencies.
One very interesting application of Fourier optics is to spatial filtering. The setup is shown in the figure. The transform lens Lt and the imaging lens Li are well-corrected achromats, here assumed to have the same focal length f. The illumination is collimated monochromatic light. When this was provided by a pinhole and collimator, it was very difficult to get sufficient intensity. Laser sources overcome this problem very well. The lenses are located a distance 2f apart. The object, a transparency, is placed a distance f in front of Lt. An inverted image of this object is formed in the focal plane of Li. The spatial Fourier transform of the object is formed in the transform plane in the focal plane of Lt. So far as forming the transform is concerned, the object can be at any location in front of Lt, since the illumination is parallel. The only difficulty is that the farther it is from Lt, the smaller is the angular aperture for the diffracted rays to enter Lt. We locate it so that Li inverts the transform in its focal plane, where the image is formed. By the use of a mask in the transform plane, we may block out any undesired spatial frequencies.
For example, if the object is crossed by a grid of equally-spaced parallel lines, this will cause a line of distinct spots along a line perpendicular to the grid and passing through the centre of the transform. If a mask blocks off these spots, the image will not contain the grid. Another striking example was that of a square grid of wires with bits of dust here and there. The dust formed a diffuse cloud near the origin. When a mask blocked off this cloud, the image was of a clean grid.
This process can be carried out by digital computation, as is commonly done for signals that are a function of time. The two-dimensional nature of the spatial case makes computation much more time-consuming, while the optical method is very fast. This is of importance in kinetic or real-time observations.
In 1665, Robert Hooke studied the shadow of the gases rising from a candle flame in parallel light. This is the basis of the shadowgraph for making density differences in a gas visible. A much more sensitive device was created by A. Toepler in 1864 for studying inhomogenieties in optical glass, which was based on the Foucault knife-edge test for concave mirrors. This test introduces a point source at the centre of curvature of a mirror (by means of a small mirror) and intercepts the returned rays where they come to a focus with a knife edge, which is adjusted to intercept about half the returned light. A perfect mirror shows an evenly illuminated surface, a paraboloidal mirror a characteristic toroidal patttern. In Toepler's device, a slit is imaged by two lenses so that there is parallel light between the lenses, and a knife edge is placed at the image of the slit to intercept a good deal of the undeviated light. This greatly increases the contrast with the light deviated by density differences in the gas. This is the schlieren apparatus, which was applied at about the same time by Ernst Mach to aerodynamic studies. It looks somewhat like a spatial filtering setup, but spatial filtering and diffraction are not involved here in any direct way (Hecht and Zajac seem to imply that they are, on p. 480). The camera lens, or the eye, behind the knife edge, is focused on the gas in the test region. The use of coherent illumination (laser) allows a variety of other arrangments, in which the knife edge is replaced by other filters. In the method of synthetic schlieren, a photograph is taken of a special pattern through the gas under study, and this pattern is analyzed mathematically to determine the density differences.
References
M. Born and E. Wolf, Principles of Optics (London: Pergamon Press, 1959). Chapter 8.
F. A. Jenkins and H. E. white, Fundamentals of Optics, 2nd ed. (New York: McGraw-Hill, 1950). Chapter 18.
E. Hecht and A. Zajac, Optics (Reading, MA: Addison-Wesley, 1974). Chapters 9-11, 14.
M. Abraham and R. Becker, The Classical Theory of Electricity and Magnetism, 2nd English edition (New York: Hafner, 1949). Includes vector fields and uses cgs units. An excellent and famous intermediate text.
C. H. Palmer, Optics Experiments and Demonstrations (Baltimore: Johns Hopkins Press, 1962). This is a remarkably excellent collection of experiments, full of ingenuity and interest. Unfortunately, it may be long out of print. For the triangle interferometer, see J. Opt. Soc. Am., v. 49, pp. 232-234, 732, and 1105-1106 (1959).
Scientific American Magazine, Light and Its Uses (San Francisco: W. H. Freeman & Co., 1980). Reprints of articles by C. L. Stong from The Amateur Scientist column, 1952-1980. Contains very challenging projects for the home experimenter (such as building your own CO2 laser). Most of the supplies are no longer easily available, since the departure of Edmund Scientific from this field. These days, one cannot even buy razor blades at the supermarket. It would be interesting to know how many people successfully completed any of these projects. Of course, the original projects were probably successful, but the experimenters were probably highly skilled (and mostly from outside the U.S.). Nevertheless, the projects are very interesting and give many ideas.
M. Minnaert, The Nature of Light and Colour in the Open Air (New York: Dover, 1954).
Return to Optics Index
Composed by J. B. Calvert
Created 26 August 2007
Last revised
 For treating diffraction at a straight edge, a slit or an opaque strip, it is useful to consider a cylindrical wavefront. In the figure, S is a slit source emitting a cylindrical wave of radius a. P is the observation point, which is at a distance b from the point V on the wavefront on the line joining S and P. We can choose any convenient value of a; here, V could be the upper edge of a screen that blocks off the wavefront below it. An element ds of the wavefront is assumed to emit a cylindrical wavelet, and the amplitude at P is the sum of the amplitudes of all visible wavelets at P. The wavelet emitted from V travels a distance b to P, while that from ds travels a distance b + Δ = d. Δ is the additional retardation of this wavelet with respect to the direct one from V.
For treating diffraction at a straight edge, a slit or an opaque strip, it is useful to consider a cylindrical wavefront. In the figure, S is a slit source emitting a cylindrical wave of radius a. P is the observation point, which is at a distance b from the point V on the wavefront on the line joining S and P. We can choose any convenient value of a; here, V could be the upper edge of a screen that blocks off the wavefront below it. An element ds of the wavefront is assumed to emit a cylindrical wavelet, and the amplitude at P is the sum of the amplitudes of all visible wavelets at P. The wavelet emitted from V travels a distance b to P, while that from ds travels a distance b + Δ = d. Δ is the additional retardation of this wavelet with respect to the direct one from V. Since the intensity is proportional to S2 + C2, a line drawn between any two points on the spiral is the amplitude corresponding to integration between the two values of v. For example, v = 0 to v = ∞ corresponds to the entire wavefront above a straight edge screen. This is a vector from (0,0) to (1/2,1/2), of length 1/√2. The whole wavefront corresponds to the line from (-1/2,-1/2) to (1/2,1/2), of length √2. Since intensities are proportional to the squares of amplitudes, the whole wavefront gives 2, while the upper half gives 1/2, or 1/4 of the unobstructed intensity, as is observed.
Since the intensity is proportional to S2 + C2, a line drawn between any two points on the spiral is the amplitude corresponding to integration between the two values of v. For example, v = 0 to v = ∞ corresponds to the entire wavefront above a straight edge screen. This is a vector from (0,0) to (1/2,1/2), of length 1/√2. The whole wavefront corresponds to the line from (-1/2,-1/2) to (1/2,1/2), of length √2. Since intensities are proportional to the squares of amplitudes, the whole wavefront gives 2, while the upper half gives 1/2, or 1/4 of the unobstructed intensity, as is observed. A cross-section showing phase relationships at the shadow boundary is shown at the right. The fringes above the boundary can be considered as due to the interference of the unobstructed wave with the edge wave; this gives the correct distribution of intensity. Below the boundary, the intensity decreases monotonically to zero. The edge wave exists in other geometries as well. It explains the Poisson-Arago spot in the centre of the shadow of a disc, as well as the faint concentric rings surrounding it.
A cross-section showing phase relationships at the shadow boundary is shown at the right. The fringes above the boundary can be considered as due to the interference of the unobstructed wave with the edge wave; this gives the correct distribution of intensity. Below the boundary, the intensity decreases monotonically to zero. The edge wave exists in other geometries as well. It explains the Poisson-Arago spot in the centre of the shadow of a disc, as well as the faint concentric rings surrounding it.
 Let's begin with a single slit of width a, illuminated by collimated light. At an angle θ = 0, all the wavelets from a wavefront are brought together at the focal point F, and the total amplitude may be denoted by Ro, and the intensity will be Io = Ro2. At an angle θ, wavelets from the bottom of the slit will travel an extra distance a sin θ with respect to those from the top. This corresponds to a phase difference of 2β = 2πa sin θ/&lambda. The plot of the resultant amplitude as we go from top to bottom of the slit will be a circular arc, subtending an angle of 2β, and of total length Ro. The vibration curve is a circle, because the phase difference is proportional to the length of the curve, as in s = rθ. If R is the length of the chord, the resultant amplitude for the whole slit, and r is the radius of the arc, then R = 2r sin β. However, Ro = rβ, so r can be eliminated and we find R = Ro(sin β/β) or R = Rosinc β. This is the single-slit Fraunhofer diffraction pattern. As a becomes comparable to the wavelength, the diffracted light is distributed in a broad cone. The first minimum of R occurs when the vibration arc closes into a circle, at β = π.
Let's begin with a single slit of width a, illuminated by collimated light. At an angle θ = 0, all the wavelets from a wavefront are brought together at the focal point F, and the total amplitude may be denoted by Ro, and the intensity will be Io = Ro2. At an angle θ, wavelets from the bottom of the slit will travel an extra distance a sin θ with respect to those from the top. This corresponds to a phase difference of 2β = 2πa sin θ/&lambda. The plot of the resultant amplitude as we go from top to bottom of the slit will be a circular arc, subtending an angle of 2β, and of total length Ro. The vibration curve is a circle, because the phase difference is proportional to the length of the curve, as in s = rθ. If R is the length of the chord, the resultant amplitude for the whole slit, and r is the radius of the arc, then R = 2r sin β. However, Ro = rβ, so r can be eliminated and we find R = Ro(sin β/β) or R = Rosinc β. This is the single-slit Fraunhofer diffraction pattern. As a becomes comparable to the wavelength, the diffracted light is distributed in a broad cone. The first minimum of R occurs when the vibration arc closes into a circle, at β = π.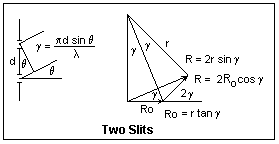 Now suppose we have two narrow slits separated by a distance d. The Fraunhofer pattern is two-beam interference, as we already know, and the fringe visibility is unity. The extra distance travelled by the light from the lower slit is d sin θ, so the phase difference is 2πd sin θ/λ = 2γ. The vibration diagram consists of two vectors of length Ro making an angle of 2γ with each other, and R is their vector sum. From the isosceles triangle thus formed, it is simple to see that R = 2Ro cos γ. We can make this more like the single-slit analysis by considering R as the third side of an isosceles triangle with equal sides r and angle 2γ. Then, R = 2r sin γ and Ro = r tan γ, from which we find the same result on eliminating r. We have not included the effect of obliquity on the amplitudes of the interfering waves. This can be done by multiplying by the factor sin β/&beta. Note that each amplitude Ro is the chord of a circular vibration arc.
Now suppose we have two narrow slits separated by a distance d. The Fraunhofer pattern is two-beam interference, as we already know, and the fringe visibility is unity. The extra distance travelled by the light from the lower slit is d sin θ, so the phase difference is 2πd sin θ/λ = 2γ. The vibration diagram consists of two vectors of length Ro making an angle of 2γ with each other, and R is their vector sum. From the isosceles triangle thus formed, it is simple to see that R = 2Ro cos γ. We can make this more like the single-slit analysis by considering R as the third side of an isosceles triangle with equal sides r and angle 2γ. Then, R = 2r sin γ and Ro = r tan γ, from which we find the same result on eliminating r. We have not included the effect of obliquity on the amplitudes of the interfering waves. This can be done by multiplying by the factor sin β/&beta. Note that each amplitude Ro is the chord of a circular vibration arc. It is not difficult now to leap to the case of a large number N of slits of spacing d. The vibration curve is a polygon that approximates the arc of a circle, and the closing side of the polygon is the desired amplitude R. The angle between each elementary vector and the next is 2γ, so the total angle subtended by R is 2Nγ. If r is the radius of the circle, then R = 2r sin Nγ, while Ro = 2r sin γ. Therefore, R = Rosin Nγ/sin γ. As γ approaches zero, R = RoNγ/γ = NRo. Therefore, the maximum intensity is Im = N2Io, where Io is the intensity due to a single slit. The same holds for γ = mπ. These are the principal maxima. The first principal maximum is at θ = 0, whatever the value of λ, but the positions of the succeeding ones depend on the wavelength. As in the case of the double slit, the maximum of order m corresponds to m wavelengths path difference between two successive slits. It is usual to multiply the expression for the amplitude by the single-slit factor sin β/β to account for the diffractive spread of the light. In most cases, the factor (sin β/β)2 in the intensity is at best a rough approximation, since the grooves are not regular slits of width a.
It is not difficult now to leap to the case of a large number N of slits of spacing d. The vibration curve is a polygon that approximates the arc of a circle, and the closing side of the polygon is the desired amplitude R. The angle between each elementary vector and the next is 2γ, so the total angle subtended by R is 2Nγ. If r is the radius of the circle, then R = 2r sin Nγ, while Ro = 2r sin γ. Therefore, R = Rosin Nγ/sin γ. As γ approaches zero, R = RoNγ/γ = NRo. Therefore, the maximum intensity is Im = N2Io, where Io is the intensity due to a single slit. The same holds for γ = mπ. These are the principal maxima. The first principal maximum is at θ = 0, whatever the value of λ, but the positions of the succeeding ones depend on the wavelength. As in the case of the double slit, the maximum of order m corresponds to m wavelengths path difference between two successive slits. It is usual to multiply the expression for the amplitude by the single-slit factor sin β/β to account for the diffractive spread of the light. In most cases, the factor (sin β/β)2 in the intensity is at best a rough approximation, since the grooves are not regular slits of width a. The most common mounting (as it is called) for a plane reflecting grating is the Littrow. The slit
S and plate P or other recording medium are placed one above the other at one end. At the other, a good achromatic lens L is placed in front of the grating, which can be rotated to select the wavelength interval received on the plate. The incident and diffracted light trace the same path in opposite directions. A small transmission grating can replace the prism in a spectrometer, where the angles can be accurately measured.
The most common mounting (as it is called) for a plane reflecting grating is the Littrow. The slit
S and plate P or other recording medium are placed one above the other at one end. At the other, a good achromatic lens L is placed in front of the grating, which can be rotated to select the wavelength interval received on the plate. The incident and diffracted light trace the same path in opposite directions. A small transmission grating can replace the prism in a spectrometer, where the angles can be accurately measured. The most pleasing of these arrangments is Lloyd's Mirror, which appeared in 1834 and is illustrated at the right. The slit S is placed a short distance above the level of the mirror; reflection in the mirror produces the image slit, and the beams from these two sources interfere. One wave is direct, the other reflected in the mirror. The mirror is simply a flat piece of glass, since the reflection at glancing incidence is nearly complete, so silvering is not necessary, and would even be deleterious, since reflection at a metal surface is not as simple as reflection from a dielectric surface. The fringes are usually observed near the end of the mirror with a telescope. The mirror may be about 30-40 mm wide and 300 mm long. If a thermal light source is used, a condenser lens may be used in front of the slit to increase the intensity. A laser source must be diverged, but a slit is not then required. The reflected wave undergoes a rare-to-dense reflection, so its phase is changed by 180°, for either polarization. The fringe at the mirror surface is then a dark fringe, which can be easily seen.
The most pleasing of these arrangments is Lloyd's Mirror, which appeared in 1834 and is illustrated at the right. The slit S is placed a short distance above the level of the mirror; reflection in the mirror produces the image slit, and the beams from these two sources interfere. One wave is direct, the other reflected in the mirror. The mirror is simply a flat piece of glass, since the reflection at glancing incidence is nearly complete, so silvering is not necessary, and would even be deleterious, since reflection at a metal surface is not as simple as reflection from a dielectric surface. The fringes are usually observed near the end of the mirror with a telescope. The mirror may be about 30-40 mm wide and 300 mm long. If a thermal light source is used, a condenser lens may be used in front of the slit to increase the intensity. A laser source must be diverged, but a slit is not then required. The reflected wave undergoes a rare-to-dense reflection, so its phase is changed by 180°, for either polarization. The fringe at the mirror surface is then a dark fringe, which can be easily seen. Let's look at the Fraunhofer pattern from two small apertures S1 and S2, as shown at the right. Each aperture alone would produce something like the Airy pattern from a disc of diameter w. This has a central bright lobe with the first minimum at an angle 1.22λ/w, where λ is the wavelength of the light used. Let P(x,y) be a typical point on a screen, with d1 and d2 the distances from P to the sources. Applying Pythagoras' Theorem, we find d22 - d12 = 2ay, where a is the distance between the sources. This shows that d2 - d1 = 2ay/(d2 + d1). If z is large compared to the other distances involved, the sum of the distances is approximately 2d, where d is the distance from the midpoint of the line joining the sources. Then we have simply Δd = ay/d = a sin θ, just as in the case of two slits. Therefore, the Airy disc is crossed by parallel fringes, that may be white light fringes. The fringes are not curved, as might be expected.
Let's look at the Fraunhofer pattern from two small apertures S1 and S2, as shown at the right. Each aperture alone would produce something like the Airy pattern from a disc of diameter w. This has a central bright lobe with the first minimum at an angle 1.22λ/w, where λ is the wavelength of the light used. Let P(x,y) be a typical point on a screen, with d1 and d2 the distances from P to the sources. Applying Pythagoras' Theorem, we find d22 - d12 = 2ay, where a is the distance between the sources. This shows that d2 - d1 = 2ay/(d2 + d1). If z is large compared to the other distances involved, the sum of the distances is approximately 2d, where d is the distance from the midpoint of the line joining the sources. Then we have simply Δd = ay/d = a sin θ, just as in the case of two slits. Therefore, the Airy disc is crossed by parallel fringes, that may be white light fringes. The fringes are not curved, as might be expected. The Michelson Interferometer, illustrated at the left, is a simple and elegant two-beam interference arrangement, apparently suggested by the requirements of the ether drift experiment first performed by Michelson and Morley in 1887, that the two light paths be at right angles. It is a "meter" because mirror M1 can be moved with an accurate screw to change the length of one of the two paths.
The Michelson Interferometer, illustrated at the left, is a simple and elegant two-beam interference arrangement, apparently suggested by the requirements of the ether drift experiment first performed by Michelson and Morley in 1887, that the two light paths be at right angles. It is a "meter" because mirror M1 can be moved with an accurate screw to change the length of one of the two paths. Two interesting interferometer arrangements are illustrated at the right. The two paths in the Mach-Zehnder are not only well-separated, but are also traversed in one direction only, so it is easy to compare conditions along one path with the other. For example, one beam can pass through a wind tunnel and be compared with an unmodified beam to detect density differences. This should be distinguished from schlieren methods that depend on refraction by the density differences and not interference. These will be described later. The Mach-Zehnder is very difficult to adjust, and must be very carefully put together. The two paths must agree to lengths comparable to wavelengths of light. The second beamsplitter B2 is really a beam combiner. Depending on the application, an extended or a point source may be used. Note that rotating beamsplitter B1 lengthens one path and shortens the other.
Two interesting interferometer arrangements are illustrated at the right. The two paths in the Mach-Zehnder are not only well-separated, but are also traversed in one direction only, so it is easy to compare conditions along one path with the other. For example, one beam can pass through a wind tunnel and be compared with an unmodified beam to detect density differences. This should be distinguished from schlieren methods that depend on refraction by the density differences and not interference. These will be described later. The Mach-Zehnder is very difficult to adjust, and must be very carefully put together. The two paths must agree to lengths comparable to wavelengths of light. The second beamsplitter B2 is really a beam combiner. Depending on the application, an extended or a point source may be used. Note that rotating beamsplitter B1 lengthens one path and shortens the other. A form of the Sagnac interferometer is shown at the right, where it is called a triangle interferometer. Another name is cyclic interferometer. The light paths are like a 45-degree triangle, while the Sagnac interferometer is usually an equilateral triangle. There will be very little difference in the functioning. The source S may be a diffuse (broad) source, or a point or collimated source. The fringes are viewed at E. When the interferometer is in perfect adjustment, the light paths are symmetrical, and the clockwise and anticlockwise paths are equal in length, whatever the angle at which the light enters, as shown. This explains why the instrument is so easy to align. The mirrors do not have to be moved, only rotated. When the main images of the source are made to coincide, the instrument will be close enough to adjustment that white-light fringes can be seen at once. In the Michelson interferometer, not only must the mirrors be parallel, but also must be at the correct distances for path equality. Monochromatic light is necessary for the alignment procedure in this case.
A form of the Sagnac interferometer is shown at the right, where it is called a triangle interferometer. Another name is cyclic interferometer. The light paths are like a 45-degree triangle, while the Sagnac interferometer is usually an equilateral triangle. There will be very little difference in the functioning. The source S may be a diffuse (broad) source, or a point or collimated source. The fringes are viewed at E. When the interferometer is in perfect adjustment, the light paths are symmetrical, and the clockwise and anticlockwise paths are equal in length, whatever the angle at which the light enters, as shown. This explains why the instrument is so easy to align. The mirrors do not have to be moved, only rotated. When the main images of the source are made to coincide, the instrument will be close enough to adjustment that white-light fringes can be seen at once. In the Michelson interferometer, not only must the mirrors be parallel, but also must be at the correct distances for path equality. Monochromatic light is necessary for the alignment procedure in this case. The Jamin refractometer is illustrated at the left. It is a two-beam interferometer specially for measuring the index of refraction of a gas. The gas is introduced into T1 or T2, while the compensator C is rotated to keep the zero-order white light fringes seen through the telescope at E in the same location. C is calibrated in index of refraction. It consists of glass plates in each beam, inclined in different directions. There are several interesting features of this interferometer.
The Jamin refractometer is illustrated at the left. It is a two-beam interferometer specially for measuring the index of refraction of a gas. The gas is introduced into T1 or T2, while the compensator C is rotated to keep the zero-order white light fringes seen through the telescope at E in the same location. C is calibrated in index of refraction. It consists of glass plates in each beam, inclined in different directions. There are several interesting features of this interferometer. Let us now relate the Fourier transform to Fraunhofer diffraction, by considering the simple case of a single slit of width a, coherently illuminated. In the figure, x is measured positive downward from the top of the slit. Light diffracted in the direction θ is brought to a focus at the point P on a screen at the focal plane of a lens close to the aperture (this lens is not shown). The phase of the light diffracted from dx at a distance x relative to that at the top of the slit is 2πx sin θ/&lambda. Summing the contributions at point P, we get a resultant amplitude A = ∫(0,a)dx exp(2πix sin θ/λ, or A = ∫(0,a)dx exp(2πipx), where the spatial frequency p = sin θ/λ = X/fλ, to a good approximation. We have neglected the usual factors before the integral that do not affect the relative intensities. If we define the aperture function a(x) to be unity for x from 0 to a, and zero elsewhere, then the amplitude is A(p) = ∫a(x)exp(2πipx), just the Fourier transform of a(x). This is the desired result.
Let us now relate the Fourier transform to Fraunhofer diffraction, by considering the simple case of a single slit of width a, coherently illuminated. In the figure, x is measured positive downward from the top of the slit. Light diffracted in the direction θ is brought to a focus at the point P on a screen at the focal plane of a lens close to the aperture (this lens is not shown). The phase of the light diffracted from dx at a distance x relative to that at the top of the slit is 2πx sin θ/&lambda. Summing the contributions at point P, we get a resultant amplitude A = ∫(0,a)dx exp(2πix sin θ/λ, or A = ∫(0,a)dx exp(2πipx), where the spatial frequency p = sin θ/λ = X/fλ, to a good approximation. We have neglected the usual factors before the integral that do not affect the relative intensities. If we define the aperture function a(x) to be unity for x from 0 to a, and zero elsewhere, then the amplitude is A(p) = ∫a(x)exp(2πipx), just the Fourier transform of a(x). This is the desired result. In two dimensions, F(p,q) = ∫∫f(x,y)exp[2πi(px + qy)]dx dy. The diffraction pattern of the rectangular aperture is easily found, depending on the two spatial frequencies p = X/fλ and q = Y/fλ, where (X,Y) is a point on the screen. A more interesting problem is a circular aperture, where f(x,y) = 1 for r≤a, 0 otherwise. Using polar coordinates, we have x = r cos θ, y = r sin θ, p = k cos α and q = k sin α. k is a radial spatial frequency. When these expressions are substituted in the transform integral, we have F(k,α) = ∫(0,a)∫(0,2π)exp[2πkr cos(θ - α)]rdrdθ. From the circular symmetry, we see that F will be independent of α, so we might as well choose α = 0. The theta integral can be found in integral tables. In fact, ∫(0,2π)exp[2πikrcos(theta;)] = 2πJ0(2πkr). Now F(k,α) = 2π∫(0,a) rJ0(2πkr)dr, which also is easy to do from tables. The result is, finall, F(k,α) = 2πa2 [J1(2πka)/2πka]. The square of this is the intensity, which, of course, is the familiar Airy disc, which is illustrated above. The zeros of J1(z) are at z = 3.83171, 7.01559, 10.17347, ... . The first zero is for 2πkr = 3.83171, or k = 1.2196/d, where d = 2a, the diameter of the aperture, which is comparable to the width of the single slit. The circular aperture of diameter d is a bit narrower than a slit of width d, so its diffraction pattern is a bit wider, 1.22 appearing instead of 1.00.
In two dimensions, F(p,q) = ∫∫f(x,y)exp[2πi(px + qy)]dx dy. The diffraction pattern of the rectangular aperture is easily found, depending on the two spatial frequencies p = X/fλ and q = Y/fλ, where (X,Y) is a point on the screen. A more interesting problem is a circular aperture, where f(x,y) = 1 for r≤a, 0 otherwise. Using polar coordinates, we have x = r cos θ, y = r sin θ, p = k cos α and q = k sin α. k is a radial spatial frequency. When these expressions are substituted in the transform integral, we have F(k,α) = ∫(0,a)∫(0,2π)exp[2πkr cos(θ - α)]rdrdθ. From the circular symmetry, we see that F will be independent of α, so we might as well choose α = 0. The theta integral can be found in integral tables. In fact, ∫(0,2π)exp[2πikrcos(theta;)] = 2πJ0(2πkr). Now F(k,α) = 2π∫(0,a) rJ0(2πkr)dr, which also is easy to do from tables. The result is, finall, F(k,α) = 2πa2 [J1(2πka)/2πka]. The square of this is the intensity, which, of course, is the familiar Airy disc, which is illustrated above. The zeros of J1(z) are at z = 3.83171, 7.01559, 10.17347, ... . The first zero is for 2πkr = 3.83171, or k = 1.2196/d, where d = 2a, the diameter of the aperture, which is comparable to the width of the single slit. The circular aperture of diameter d is a bit narrower than a slit of width d, so its diffraction pattern is a bit wider, 1.22 appearing instead of 1.00. In the figure, h(x) is shown as a sudden rise followed by a gradual decline to zero. This is not an unusual case. Since the area under the curve is finite, stability is satisfied. Causality is also clearly satisfied; there is no response before the impulse is applied at x = 0. In the middle diagram, the input f(τ) produces an output at x equal to the value of f(τ) times the value of the impulse response function at x. The inputs for other values of τ will have their appropriate contributions. Clearly, we need to consider values of f(τ) only for a limited range of τ, and, of course, none after τ = x. It should be easy to see that we get the same contribution from f(τ) by putting the origin of h(x) at x and reflecting it; the same value now falls under f(τ) as previously was at x, and all we need to do is multiply them to get the contribution of f(τ) to the output. The contribution from all values of f(τ) is then the integral of the product of these two functions. In fact, y(x) = ∫f(τ)h(x - τ)dτ. This is the convolution of f(x) and h(x), which we shall write g(x) = f(x)*h(x). The proper symbol is an X in a circle, but browsers do not support this.
In the figure, h(x) is shown as a sudden rise followed by a gradual decline to zero. This is not an unusual case. Since the area under the curve is finite, stability is satisfied. Causality is also clearly satisfied; there is no response before the impulse is applied at x = 0. In the middle diagram, the input f(τ) produces an output at x equal to the value of f(τ) times the value of the impulse response function at x. The inputs for other values of τ will have their appropriate contributions. Clearly, we need to consider values of f(τ) only for a limited range of τ, and, of course, none after τ = x. It should be easy to see that we get the same contribution from f(τ) by putting the origin of h(x) at x and reflecting it; the same value now falls under f(τ) as previously was at x, and all we need to do is multiply them to get the contribution of f(τ) to the output. The contribution from all values of f(τ) is then the integral of the product of these two functions. In fact, y(x) = ∫f(τ)h(x - τ)dτ. This is the convolution of f(x) and h(x), which we shall write g(x) = f(x)*h(x). The proper symbol is an X in a circle, but browsers do not support this. As another example, consider the convolution of a slit with itself, as shown in the figure at the right. This is easily worked out by inspection, since the slit is symmetrical about its centre, and the area of overlap is proportional to displacment. The convolution is seen to be a triangular function of twice the width of the slit. The Fourier transform of this triangular function is the square of the transform of the slit, or sinc2(πpa). This function has its zeros in the same location as for the single slit, but the side lobes are considerably less because of the squaring. If this is to be a diffraction pattern, we will need a slit of width 4a, but with amplitude attenuation varying linearly. In terms of the zeros, it is no wider than the single slit, however. This is an example of apodization, but not a particularly good one, since the side lobes are still there, if reduced in height.
As another example, consider the convolution of a slit with itself, as shown in the figure at the right. This is easily worked out by inspection, since the slit is symmetrical about its centre, and the area of overlap is proportional to displacment. The convolution is seen to be a triangular function of twice the width of the slit. The Fourier transform of this triangular function is the square of the transform of the slit, or sinc2(πpa). This function has its zeros in the same location as for the single slit, but the side lobes are considerably less because of the squaring. If this is to be a diffraction pattern, we will need a slit of width 4a, but with amplitude attenuation varying linearly. In terms of the zeros, it is no wider than the single slit, however. This is an example of apodization, but not a particularly good one, since the side lobes are still there, if reduced in height. If we choose the fundamental interval as shown, f(x) is an even function and only the cosine terms will survive. The integrals are easy to evaluate. The even harmonics vanish, while the odd harmonics remain, with amplitudes proportional to the reciprocals of odd integers and alternating signs. The powers in each harmonic are proportional to the squares of the amplitudes. Loss of the higher harmonics corresponds to rounding of the waveform. Note that the series converges to the function everwhere except at the jump discontinuities, where it converges to 1/2, the average of the limits as these points are approached from two sides. All of this is characteristic of Fourier series. The series is easily modified for an arbitrary fundmental interval and height. The term "square wave" refers to the equality of the lengths of 1 and 0 values, and the vertical discontinuities, not to the shape of the wave in a diagram.
If we choose the fundamental interval as shown, f(x) is an even function and only the cosine terms will survive. The integrals are easy to evaluate. The even harmonics vanish, while the odd harmonics remain, with amplitudes proportional to the reciprocals of odd integers and alternating signs. The powers in each harmonic are proportional to the squares of the amplitudes. Loss of the higher harmonics corresponds to rounding of the waveform. Note that the series converges to the function everwhere except at the jump discontinuities, where it converges to 1/2, the average of the limits as these points are approached from two sides. All of this is characteristic of Fourier series. The series is easily modified for an arbitrary fundmental interval and height. The term "square wave" refers to the equality of the lengths of 1 and 0 values, and the vertical discontinuities, not to the shape of the wave in a diagram. One very interesting application of Fourier optics is to spatial filtering. The setup is shown in the figure. The transform lens Lt and the imaging lens Li are well-corrected achromats, here assumed to have the same focal length f. The illumination is collimated monochromatic light. When this was provided by a pinhole and collimator, it was very difficult to get sufficient intensity. Laser sources overcome this problem very well. The lenses are located a distance 2f apart. The object, a transparency, is placed a distance f in front of Lt. An inverted image of this object is formed in the focal plane of Li. The spatial Fourier transform of the object is formed in the transform plane in the focal plane of Lt. So far as forming the transform is concerned, the object can be at any location in front of Lt, since the illumination is parallel. The only difficulty is that the farther it is from Lt, the smaller is the angular aperture for the diffracted rays to enter Lt. We locate it so that Li inverts the transform in its focal plane, where the image is formed. By the use of a mask in the transform plane, we may block out any undesired spatial frequencies.
One very interesting application of Fourier optics is to spatial filtering. The setup is shown in the figure. The transform lens Lt and the imaging lens Li are well-corrected achromats, here assumed to have the same focal length f. The illumination is collimated monochromatic light. When this was provided by a pinhole and collimator, it was very difficult to get sufficient intensity. Laser sources overcome this problem very well. The lenses are located a distance 2f apart. The object, a transparency, is placed a distance f in front of Lt. An inverted image of this object is formed in the focal plane of Li. The spatial Fourier transform of the object is formed in the transform plane in the focal plane of Lt. So far as forming the transform is concerned, the object can be at any location in front of Lt, since the illumination is parallel. The only difficulty is that the farther it is from Lt, the smaller is the angular aperture for the diffracted rays to enter Lt. We locate it so that Li inverts the transform in its focal plane, where the image is formed. By the use of a mask in the transform plane, we may block out any undesired spatial frequencies.