Open-Channel Flow

Contents

1. Introduction
2. Channel Flow
3. Flow Velocity Formulas
4. Specific Energy
5. Nonuniform Flow
6. Water Profiles
7. Hydraulic Jump
8. Channel Shapes
9. Weirs
10. References

The flow of water in an open channel is a familiar sight, whether in a natural channel like that of a river, or an artificial channel like that of an irrigation ditch. Its movment is a difficult problem when everything is considered, especially with the variability of natural channels, but in many cases the major features can be expressed in terms of only a few variables, whose behavior can be described adequately by a simple theory. The principal forces at work are those of inertia, gravity and viscosity, each of which plays an important role.

We shall consider only water as the fluid, as it is by far the most common one, and for which the most experimental data are available. Other fluids will behave in about the same way, under conditions that we shall specify below. Water has a density of about 1 g/cc or 62.3 to 62.4 pounds per cubic foot depending on the temperature, and does not vary significantly for the temperatures and pressures that we shall consider. Sea water weighs 64 pcf. In this article, I shall use mainly metric units, but may slip into foot-pound-second units now and then. The acceleration of gravity will be taken as 980 cm/s² or 32.2 ft/s². Variations in gravity with latitude and place will have very little effect, so we shall neglect them. The kinematic viscosity ν of water under normal conditions is about 0.15 cm/s². It decreases from about 0.20 at freezing to 0.0028 at the boiling point, or to 0.008 at 90°F. The figure 0.15 corresponds to about 55°F. The kinematic viscosity is the ratio of the dynamic viscosity to the density, and can be considered as the diffusion constant of momentum due to molecular motion. Since the density of water is 1, the dynamic viscosity η is 0.01 g/cm-s, numerically the same. The shear force on a surface is then τ = η(dv/dz), where dv/dz is the velocity gradient at the surface. The modulus of compressibility of water is about 300,000 psi, so water can be considered incompressible for the present purposes.

All of our results will be based on the conservation of mass, momentum and energy (in the form of Bernoulli's theorem), and the Manning formula for frictional resistance. It is amazing how far one can go on this simple basis, without appeal to the general equations of hydrodynamics or the structure of boundary layers.

The assumptions, methods and formulas that we will present here work for problems of water flows on the usual engineering scale. The flows are long compared to their cross-sections, so that a single velocity can describe the situation adequately at any cross-section. Flow depths and dimensions are larger than the thickness of boundary layers, so that the flow is completely turbulent. Sizes are large enough that capillary forces play a negligible role. Under these conditions, the analysis will normally give very good results, of an accuracy sufficient for engineering purposes. The References will lead into the extensive literature of the field.

Consider the flow of water in a channel of arbitrary shape. The area between the free surface of the water and the bed of the channel is A, which depends on the height of the water y above the bottom of the channel. An average depth d can be defined by d = A/y. It is the depth which, when multiplied by a certain height of the water, gives the area. Let the total amount of flow be Q cm³/s. A more practical unit is m³/s or ft³/s, often written cfs (the unit "second-foot" means the same as cfs, but should be deprecated). 1 m³/s = 35.31 cfs = 10⁶ cm³/s. An acre-foot is 43,560 ft³, so a flow of an acre-foot per day is 0.504 cfs. A U.S. gallon is 231 in³, so 1 cfs = 7.48 gal/s or 449 gal/min.

If we know the discharge Q and the area A, we can calculate a quantity V = Q/A with the dimensions of a velocity. If the velocity were uniform over the cross-section A, then this would be the velocity that would give the observed discharge. The velocity is actually zero at the wetted boundary of the channel, and increases to a maximum at the centre of the channel and a little distance beneath the surface. The region near the wetted boundary is called the boundary layer, and most of the change in velocity takes place across it. This means that the quantity V is close to the velocity of most of the water, and we use it as if this were true.

In fact, the kinetic energy per unit mass, v²/2g, when averaged over the cross-section, is αV²/2g, where α is a correction factor a little larger than unity (1.1 is typical), which we can use if we require more accuracy in expressing the kinetic energy in terms of V. Similarly, the average momentum per unit volume is βV, where β is a correction factor usually less than α. The approximate independence of our results on the actual velocity distribution is a consequence of the tbinness of the boundary layer. We replace all the complexity of the velocity distribution by one number, the average velocity V, and in most of our work it can even be taken to be the actual water velocity.

The surface velocity of, say, a river can be measured by timing a float placed in the center of the stream. The distance between two points established by poles on either side of the river, divided by the time required for the float to cover the distance, gives the surface velocity. The old rule of thumb was that V is 0.8 of the surface velocity. Then, if you measure the depth of the river at good points in a cross section, its flow area A is known, from which the discharge is Q = AV. Discharge is more accurately measured by a sharp-ceested weir, and approximate gauging is now done by a propeller or other device similar to an anemometer that measures the velocity at some selected point and is calibrated for the particular stream.

It's clear that water flows more rapidly the steeper the slope. On a constant slope, the velocity reaches a steady value when the gravitational force is equal to the resistance to flow. For solid bodies, the frictional force is about independent of velocity, so they just go on accelerating if they move at all, and never reach a steady state, ideally. Fluids are different. The shear force between the liquid and its bed depends on the square of its velocity, which is suggested by dimensional analysis. The frictional force per unit area is approximately τ = CρV²/2, where C/2 is just a constant that must be determined empirically. There is no physics in this; we have just used dimensional analysis and the wonder is that it turns out to be almost right. Therefore, we are pretty sure water will reach a steady velocity in flowing down an incline.

The slope S is the ratio of fall h to distance along the channel, S = h/L. In surveying, slope is usually referred to horizontal distance. In fact, the slopes of water channels are usually so small that the difference is negligible. A slope of 0.01, or 1 in 100, is a rather steep slope for a channel, and 0.001 or even less is more typical. The weight of a length L of water with cross-sectional area A is ρgAL. If the channel slopes, the component of the weight along the channel is ρgAL(h/L) = ρgAh. This has to be balanced by the force exerted by the bed of the channel, τPL, where P is the wetted perimeter of the channel. The frictional force is exerted only along this perimeter. Therefore, ρgAh = τPL = CρPLV²/2, and so V² = 2gCAh/PL = 2gCRS, where S is the slope and R = A/P is called the hydraulic radius. Then, V = C'√(RS), which is Ch&eaucte;zy's formula (1775). Note that the coefficient C' has dimensions, and so differs when different units are used. Let us agree that in the basic formula, R will be in m and V in m/s. Then, C' is on the order of 100. If we use cm, then C' = 10, and if we use feet, C' = 181.

Chézy's formula is not bad, but did not provide results that satisfied engineers. The Swiss engineers E. Ganguillet and W. R. Kutter (1869) showed that much better results could be obtained if the constant C' depended on R, S and a constant n that was characteristic of the roughness of the channel as follows: C' = (23 + 0.00155/S + 1/n)/[1 + n(23 + 0.00155/S)n/√R]. This, of course, is for metres. For feet, it is multiplied by 1.811, and the parenthesis in the denominator is also multiplied by 1.811. As an example, consider a smooth iron pipe for which n = 0.011, S = 0.001 and R = 1.0 m. Kutter's formula gives C' = 90.9, and V = 2.87 m/s. For many channels of metal, concrete and wood, n = 0.011 to 0.017. For canals in earth and smooth natural channels, n = 0.025 to 0.033, while for weedy streams, n = 0.075 to 0.150. This will give some idea of the variation of n. Better values can be found in engineering references.

Kutter's formula works well, but is very difficult to use in iterative and theoretical calculations because it cannot be solved for R or S easily. Manning found a formula that gives results very close to Kutter's, but is much simpler, and which is now used almost exclusively. Manning's formula (1890) is V = R^2/3S^1/2/n, where n is the same as in Kutter's formula. It is absolutely remarkable that such a simple formula gives such good results, and that it uses the same roughness parameter n. Working the same example as in the preceding paragraph, we find V = 2.87 m/s, so the agreement is excellent. Manning's formula is easily solved for R or S, a great advantage. If you use feet, multiply by 1.49.

Let us use a simple rectangular channel as an example. Many channels are actually rectangular, or close to it, so this is a useful example. We will show the modifications necessary when the channel is not rectangular, and will note that the results are pretty much the same qualitatively. Let y be the depth of the water above the bottom of the channel, and b the width of the channel. Then its area is yb, and its wetted perimeter is b + 2y, so its hydraulic radius is yb/(b + 2y). The discharge is Q = AV = byV, or the discharge per unit width is q = Q/b = yV. Using Manning's formula, q = y[yb/(b + 2y)]^2/3S^1/2/n. Now, if we know y, R and S we can just substitute in the equation and find q. In many problems, however, we are given some desired discharge, and want to find the corresponding y and V. This was once an arduous process, involving an iterative solution. Now, with a tool like the HP-48G, it is straightforward. Use the SOLVE facility. All you have to do is express the equation in terms of numbers and the variable y, type it in, and press SOLVE. Even in Daugherty's excellent and accurate text, on p. 313 this is done manually with an incorrect result, 2.17 ft instead of 2.47 ft. The HP-48 not only saves work, but more importantly it is less subject to error.

Many of our illustrations will be for an even simpler example, the wide rectangular channel in which only bottom friction is present. If b is the width of the channel (b >> y) then the discharge per unit width is q = Q/b. The area A = by, and the wetted perimeter is b, so R = y. Results for the wide rectangular channel will be similar to those for a channel of any shape.

Given S and Q, and the shape of the channel, we can find y and V; given S and y, we can find Q. If we do not have a rectangular channel, but one of arbitrary shape, we must work with Q instead of q, and y is usually the depth from the lowest point in the channel. Then the area A occupied by fluid and the wetted perimeter P are functions of y, which may be expressed analytically for channels of a geometric shape. Then, R can be expressed as a function of y, and used in the Manning equation. We have, in fact, done this for the rectangular channel. All we have to do is replace the square bracket above by R(y). If R is expressed as, say, a table of values, the best way to proceed is to plot or tabulate q as a function of y, and then enter the table with q instead of y. You should feel comfortable with these calculations after a little practice. They can solve many problems all by themselves. The value of y corresponding to a given Q and S is called the normal depth for those conditions.

Williams and Hazen's formula, V = 1.32CR^0.63S^0.54 is for nonferrous pipe. C = 120 for bad, 130 for average, and 140 for new pipe. The formula also applies to rock tunnels, with C = 38 for bad, 45 for ordinary and 50 for best. For steel pipe, Scobey's formula is V = CR^0.58S^0.526, with C = 154 for smooth welded pipe, 120 for riveted. These empirical formulas are quite close to Manning's, and not too far even from Chézy's.

Bernoulli's theorem expresses the energy content of unit volume of fluid as U = ρgz + p + ρV²/2, and states that it is constant along a streamline in the absence of dissipation. It is usually more convenient to express the terms as lengths, or "heads," by dividing by γ = ρg: H = z + p/γ + V²/2g. The three energy components are elevation, pressure, and velocity. All play a role in open-channel flow. For any flow, there is an energy grade line that can be imagined above the flow, and its slope is S'. The water surface is the hydraulic grade line (HGL), which is below the energy grade line by the velocity head V²/2g. Below this is the bed grade line, with slope S, and (usually) below that is the horizontal datum, the reference surface.

The streamlines of the flow are parallel. Along any streamline, z + p/γ + V²/2g is a constant. Let us now assume z is the elevation of the bottom streamline, so that if the flow depth is y, the elevation of the surface streamline is z + y. The gauge pressure here is zero, so Bernoulli's Equation for this streamline is z + y + V²/2g = C. Now for the bottom streamline, the gauge pressure is γy, so that p/γ = y, and Bernoulli's equation is z + y + V² = C, where C has the same value as for the top streamline. At any intermediate height y', z + y' + γ(y - y')/γ + V²/2g = C. Therefore, C, the energy per unit weight, has the same value at any depth. The part y + V²/2g is called the specific energy E, and is the energy per unit weight referred to the stream bed.

When a closed channel runs full, then the depth can no longer vary to accommodate the discharge, and the pressure becomes different from the atmospheric pressure, and must be taken into account in using Bernoulli's theorem. This is the fundamental difference between open channel flow and pipe flow.

We can express E as a function of Q easily, using Q = AV: E = y + Q²/2gA². For simplicity, consider a rectangular channelof width b, for which A = by. Then E = y + q²/2gy², expressing E as a function of the discharge q and the depth y, or q = y√[2g(E - y)], expressing q as a function of E and y.

The curve of q as a function of y for a fixed E is plotted at the right. We notice that q is a double-valued function of y, and has a maximum possible value q_m. The corresponding depth y can be found by differentiating q with respect to y and setting the derivative equal to zero. The result is y_c = 2E/3, called the critical depth. The corresponding value of q, q_m = √(gy_c³) is the critical flow, and V_c = q_c/y_c is the critical velocity. For depths greater than the critical depth, the velocity is smaller than the critical velocity. Flow in this region is called subcritical. For depths smaller than the critical depth, the velocity is greater than the critical velocity. Flow in this region is called supercritical. Note that the sub- and super- refer to the velocity of flow. The same discharge q is possible with given E in either region. In the upper region, we have greater flow area, in the lower region greater flow velocity. Because the frictional resistance varies rapidly with velocity, subcritical uniform flow is associated with gentle slopes, supercritical uniform flow with steep slopes.

Note that the curve is plotted with respect to dimensionless variables, so the same curve can be used for any E or q_m. Consider flows described by points a and c. Since they are on the same vertical line, the discharge is the same for each. The distance from the y = 0 axis to point a corresponds to the static part of E, while the distance from a to the y = E line corresponds to the kinetic energy, which sum to E. The same holds for point c, but here the static part is much smaller and the dynamic part larger. At the point of maximum discharge for this value of E, point e, the static energy is twice the dynamic energy.

Suppose that there is a lateral constriction in the channel, reducing its area so that q/q_m increases from 0.6 to 0.8. Assume there is no head loss, the specific energy does not change, so the flows in the constriction are represented by points b and d. We note that in subcritical flow, the depth of flow decreases, while in supercritical flow the depth increases.

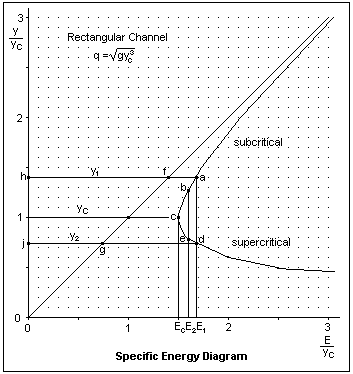We can also plot y/y_c as a function of E for a constant discharge q, as shown at the left. Again, this is for a rectangular channel but diagrams for other channel shapes are similar. This curve is also plotted with dimensionless variables, E/y_c vs. y/y_c, so it can be used for any discharge. The critical depth y_c = (q²/g)^1/3, where q is the discharge per unit width. If x = y/y_c, then E/y_c = x + 1/2x². Critical depth corresponds to y/y_c = 1, for which E/y_c = 3/2. The point a corresponds to an upper-stage or tranquil flow. Line segment hf represents y/y_c, while line segment fa represents the kinetic energy V²/2gy_c. Note that the specific energy is a minimum at the critical depth. This minimum value will, of course, depend on the discharge.

Let us suppose there is a hump in the bed of the channel that decreases the specific energy from E₁ to E₂. The height of the hump will be the decrease in the specific energy. If the flow is subcritical, we see that depth will decrease slightly to point b. If the flow is supercritical, the depth will, on the other hand, increase slightly to point e. This is exactly the same as the response to a lateral constriction. If the hump is high enough, the flow may become critical at it. For any larger hump, the specific energy cannot decrease further, and instead the upstream depth must increase to keep the flow critical over the hump. For this reason, such a point may be called a control section, since it controls the upstream depth. The vertical tangent at critical depth means that small changes in E will cause large changes in y, so the surface may appear disturbed.

On any declining slope S, uniform flow will be established (if possible) at a depth y called the normal depth for a given Q. If the normal depth is greater than the critical depth, then the slope S is called mild and the flow tranquil or upper-stage. If it is smaller, then the slope S is called steep and the flow is called rapid or lower-stage. (or, of course, subcritical or supercritical.) Whether a slope is mild or steep depends on Q and n, the discharge and roughness. A slope giving exactly the critical velocity is called, unsurprisingly, critical, and is not often found. There are also horizontal (S = 0) and adverse (S < 0) slopes, on which uniform flow is not possible, but such slopes are always of limited extent.

Since y_c = 2E/3 and E = y + V²/2g, it is easy to see that V²/2g = y_c/2, or V_c = √(gy_c). Since q = y√[2g(E - y)], we find q_max = √(gy_c³). That this is indeed the maximum q for the given E can be found by setting dq/dy = 0 and solving for y, with the result y = y_c. Maximum discharge occurs for critical flow.

We also note that V_c²/gy_c = 1. The dimensionless term V/√(gy) is called the Froude number F. It expresses the relative strength of inertial and gravitational forces, and was first used in ship modelling in the estimation of wave drag effects. If the Froude numbers of two flows are the same, then these effects will be similar. In the present case, F = 1 corresponds to critical flow, F < 1 to subcritical flow, and F > 1 to supercritical flow.

The Reynolds number of an open-channel flow is defined as Re = 4RV/ν, where the kinematic viscosity ν has been given above. It expresses the ratio of inertial forces to viscous forces. With R in m and V in m/s, Re = 2667RV. In nearly all practical cases, Re >> 1, so the flow is turbulent.

When we use specific energy, we are really using Bernoulli's principle, where the total energy H = z + E. Energy is conserved except for friction, and this causes H to decrease with distance at a rate s', so the loss of head in a distance L is h_L = Hs'L. s' can be found from Manning's formula: s' = [nV/R^2/3]². For a fixed Q, the velocity V is found from the depth y by continuity, Q = VA(y). Therefore, for any depth of water we can find the frictional head loss. If the bottom of the channel varies in elevation, then E, which is the difference between H and y + z, varies accordingly.

These ideas are summarized in the diagram at the right, which shows a reach between 1 and 2 in which the flow is uniform. The direction of flow is, of course, the direction in which the energy line (EL) falls. Note that the slope of the EL (s) is the same as the bed slope (s'). The average velocity V has adjusted itself to make this so, determining the depth y from the known specific energy E or discharge Q. This depth is the standard depth, and the velocity is the standard velocity, for this flow. The hydraulic grade line HGL is the water surface, which is also parallel to the EL and the bed. The critical depth y_c is the lower boundary of the region for which the specific energy decreases with increasing depth (subcritical flow) and the upper boundary of the region where the specific energy increases with a decrease in depth (supercritical flow). The critical depth is the solution of the equation Q²/g = A³/b, where b is the width of the water surface. For a rectangular channel of width b, Q²/g = b²y³, or y_c = [q²/g]^1/3, where q is the discharge per unit width. In the diagram, y > y_c, so the flow is subcritical.

The slope s' of the channel may be different in different reaches; the channel may change width or shape, there may be humps and hollows in the channel, or weirs and sudden drops, and other factors that change the flow conditions. The resulting flow will be steady, although the elements of the water will experience acceleration from point to point. We can usually make a good approximation to the flow by using Bernoulli's theorem and dividing the problem into lengths of approximately uniform conditions. We will want to know how the depth y and the velocity V vary with position, as well as the other characteristics of the flow. These problems are quite interesting, have many practical applications, and show the power of engineering hydraulics.

Consider a hump in the water surface, a surface wave travelling down the channel with some velocity V. That such waves exist is an experimental fact. Now suppose the water in the channel is moving with velocity V in the other direction; the wave will appear to stand still. For simplicity, suppose the channel is level, S = 0, at least for a short distance. Then, from Bernoulli's theorem, E = E', where E is the specific energy approaching the wave, and E' is the specific energy at the centre of the wave. Let the depth increase from y to y' = y + Δy, so that Δy is the amplitude of the wave. From E = E' we easily find that V²/2g = (y' - y)/[1 - (y/y')²]. Now substitute y + Δy for y', and expand in powers of Δy. The result is V = √(gy)(1 + 3Δy/4y + ...). For waves of small amplitude, the phase velocity is c = √(gy).

The general expression for the velocity of surface waves of wavelength λ is c = [(gλ/2π)tanh(2πy/λ)]^1/2 (vide Lamb, p. 364), where y is the depth of the water. The two limiting cases are shallow water (or long wavelengths), y << λ, when c² = gy, independently of the wavelength, and deep water, y >> λ, when c² = gλ/2π. In deep water (or short wavelengths), the velocity is proportional to the square root of the wavelength, as in the ocean, where waves of different periods separate themselves from each other when propagating long distances. The group velocity in this case is half the phase velocity. The propagation of gravity waves on a water surface is said to be dispersive.

We observe both kinds of waves on the surface of the water in our channels. The most important thing to us is that the speed of long surface waves is exactly the critical velocity! If the water is moving faster than the critical velocity, as in rapid flow, then wave disturbances cannot propagate upstream. An obstacle sticking up throught the surface creates a spreading wave like a supersonic bullet, with a half-angle of θ = sin^-1(V_c/V). On the other hand, in tranquil flow waves from a disturbance can propagate upstream as well as down. This is one way to determine whether an observed flow is supercritical or subcritical, by simple observation.

Suppose that the slope increases from mild to steep at a certain point. The upstream normal depth y is greater than y_c, while the downstream normal depth y' is less than y_c. The depth decreases as E decreases on the upper-stage curve, then continues to decrease as E goes through a minimum at the critical depth near the break point of the profile, and then E increases again until the normal depth for the steep slope is reached. If we try to decrease E below the minimum by raising the bed of the channel by Δz, of course E cannot decrease further, and the result will be to raise the upstream water level by Δz. Because of this, the point at which critical depth is reached is called a control section, because it controls the upstream depth.

If the slope decreases from steep to mild, something very different takes place. As y increases toward the critical depth, a flow instability occurs at some point, and the flow becomes turbulent until the new normal depth is attained downstream in tranquil flow. This is called a hydraulic jump, which will be analyzed below.

If H = z + E, then dH/dx = dz/dx + dE/dx, where x is distance along the flow. Now dH/dx = s, the slope of the energy line, and dz/dx = s', the slope of the bed of the channel. Therefore, dE/dx = s - s', where dE/dx = dy/dx + d(V²/2g)/dx. Since q = Vy = constant, Vdy + ydV = 0. Then d(V²/2g) = (V²/gy)(-dy), so s - s' = (1 - V²/gy)dy/dx = (1 - F²)dy/dx. Hence, dy/dx = (s - s')/(1 - F²). This equation tells us whether the water surface is rising or falling in the direction of motion. In uniform motion, s' = s and dy/dx = 0. For upper-stage flow, the sign of dy/dx is the same as the sign of s - s'. For lower-stage flow, the sign of dy/dx is opposite. The dimensionless parameter F is the Froude Number. F > 1 corresponds to supercritical flow, F < 1 to subcritical flow. It is analogous to the Mach Number in compressible fluid flow. It was originally defined by Froude as the speed of a ship divided by the square root of its water level length (not dimensionless). The relative wave resistances of hulls of different sizes and speeds are the the same if the Froude numbers are equal, permitting resistance tests on model ships.

The equation for dy/dx must be used with care near critical depth, since it predicts an infinite slope there. When water is flowing at critical depth, the surface is typically disturbed. However, the equation cannot account for the details of flow in this region, and, of course, the infinte slopes are not observed.

The figure at the right shows a reach in which s &neq; s'. In the case shown, s > s', so the specific energy decreases from 1 to 2. Since the flow is subcritical, this means that the depth decreases while the velocity increases. The flow is no longer uniform, but is still steady, and the discharge is constant at any cross-section. It is easy to get an expression for the change in specific energy by equating the vertical distances at 1 and 2: s'L + V₁²/2g + y₁ = y₂ + V₂²/2g + sL. This relation is usually rearranged to give the distance L, when the depths at each end of the reach are assumed: (s' - s)L = E₂ - E₁.

Suppose we have uniform subcritical flow on a mild slope, and let us modify the downstream end of the channel. One modification would be to create a dam that would raise the depth in front of it. The discharge must get by the dam somehow, either by flowing over the top or through a gate, for example. A backwater deeper than the normal depth would form that would slowly approach the normal depth as we pass upstream. Or, we could allow a free discharge from the end of the channel that would then fall as a free jet. In this case, we would have a drawdown water surface with a depth less than the normal depth, approaching normal depth as we go upstream. These surface profiles are denoted M₁ and M₂, respectively, by Bakhmeteff. If the water discharges through a gate at the bottom of a dam with water behind it at greater than critical depth, its velocity will be greater than critical. The depth will then rise as the water decelerates because of the large resistance. Before it reaches critical depth, a hydraulic jump will occur, making the transition to subcritical flow. The resulting profile is denoted M₃. The water profile can be calculated by the formula just derived, starting from some point where the depth is known and finding the distances to points where the depth takes a series of increments approaching the normal depth.

On a steep slope, the normal depth is less than the critical depth, so the water profiles are different from those on a mild slope. If the depth is greater than the normal depth (but less than the critical depth), it will approach the normal depth as it accelerates downstream, while if the depth is less than normal depth, the water will decelerate with increasing depth, approaching normal depth asymptotically. These are the profiles S₂ and S₃, respectively. A supercritical flow approaching a dam will undergo a hydraulic jump and become subcritical, then rise on the steep slope with a backwater curve designated S₁. Downstream influences do not affect upstream flows when the velocity is supercritical. In particular, there will be no drawdown curve approaching a free exit.

These six flow regimes cover most applications, but special profiles can be identified for critical slopes (normal and critical depths equal), and for horizontal and adverse slopes (normal depth infinite). The profiles for horizontal and adverse slopes are similar to those for a mild slope with an infinite depth, but of course normal uniform flow is not possible. Diagrams of these profiles are shown in Daugherty and Franzini (p. 306), and in Urquhart (p. 4-90).

When the channel slope changes from mild to steep, the initially uniform subcritical flow must change to the finally uniform supercritical flow, while the flow velocity accelerates from its initial value to its final value. This transition is smooth and efficient, with little additional loss of head, like converging flow in a pipe. In the region of acceleration on the mild slope, the velocity is higher than its normal value, so the rate of head loss is greater. The energy line now approaches the profile line, so that the specific energy (which is the vertical distance between them) decreases. From the specific energy diagram, we see that the flow depth decreases as a result. At the break in bed slope, the flow velocity is less than the normal value, so the resistance is less, and the energy line and profile line now diverge, and the specific energy increases. The point of the break, then, is the point of minimum specific energy, and the corresponding depth of flow is the critical depth for the given discharge. Because of the rapid change of depth with specific energy (vertical tangent to the specific energy curve) there may be surface disturbances at this point. As the specific energy increases further on, the depth of flow decreases until it finally approaches the normal depth for the profile gradient. Similar flows occur at the outflow of reservoirs and spillways, but the location of critical depth may be somewhat further upstream. This transition is always characterized by a decrease in depth of flow in the direction of flow.

At a free outfall from a mild slope, the specific energy decreases up to the end of the channel. Nevertheless, critical depth is reached before this point, typically a distance 4y_c from the lip. The depth at the lip is about 0.7y_c. The reason for this is in the change in the flow pattern near the end. The kinetic energy factor α may decline to near 1.0 at the exit, and the curvature of the streamlines may reduce the pressure by centrifugal force. In the free jet, the velocity may well be uniform across the jet, very different from the velocity distribution in the channel. It is usually accurate enough to assume that critical depth is reached near a crest of the flow.

Let's use the relation we have just obtained to find the water levels in a practical problem. Suppose we have a rectangular channel of width b = 6 m and slope S = 0.002, which is 1 in 500, or 10.5 ft/mile. The discharge is Q = 100 cms (cubic metres per second), and the roughness is n = 0.012. The depth of steady flow y_o can be found from Manning's formula. We have 100 = (6y)(1/0.012)[6y/(6 + 2y)]^2/3(0.002)^1/2, which we solve for y = y_o. The HP-48G gives us y_o = 3.3066 m. Then V_o = 100/(6y_o) = 5.040 m/s, so E_o = 4.6028 m. The critical depth y_c = (2/3)E = 3.0685 m. Since this is less than the actual depth, the flow is tranquil or upper-stage, and the slope is mild.

It is easy to repeat the calculation for any Q. Simply edit the constant value in the equation, and use SOLVE again. For example, if Q = 10 cms, then y_o = 0.669 m, V = 2.492 m/s, E = 0.986 m and y_c = 0.657 m.

Now suppose we have placed a dam with a spillway height of 8 m above datum at the lower end of the channel. We assume that the width is the same, 6 m, for simplicity, and that the height of the water over the spillway sill will be the critical depth at that point. Since the critical velocity V_c = √(gy_c) and Q = bV_c = b√(gy_c), we can solve for y_c, with the result y_c = 3.05 m, and V_c = 5.467 m/s. The height of the energy line at this point is then 8 m + (3/2)y_c = 12.57 m.

Now we can estimate conditions at the end of the channel at the dam. We assume that y₂ = 12.57 m, neglecting the small contribution of the velocity, which is only V = 100/(12.57)(6) = 1.326 m/s. This is not quite correct, but the error will not be large, so a more detailed estimate is not worth the effort. Make a table with columns for y, A, P, R, V, V²/2g and E, for calculating the specific energy at the ends of a series of reaches upstream. For this station, the numbers are 12.57, 75.42, 31.14, 2.422, 1.326, 0.0897 12.660. Instead of trying to find the conditions at some distance L upstream, it is much easier to assume a new depth, and then find the distance L that corresponds.

Therefore, take a new depth at y₁ = 12.00 m. The columns of the table can be filled in with little trouble. The numbers are: 72.00, 30.00, 2.400, 1.389, 0.0984, 12.094. The specific energy has decreased from 12.660 m to 12.094 m in the reach, so the change in E is -0.566 m. We now calculate the slope S' of the energy line using Manning's formula. Average the velocities and the hydraulic radii at the ends of the reach. We find V = 1.358 m/s and R = 2.411 m. The energy slope that corresponds to this velocity is S' = [nV/R^2/3]² = [(0.012)(1.358)/2.411^2/3]² = 8.214 x 10^-5. Because the velocity is so low, this is really a small frictional loss. Then S - S' = 1.917 x 10^-3. Then L = 0.566/1.917 x 10^-3 = 295 m. The minus sign just means we are going upstream.

Conditions in the last reach of the channel are shown in the figure at the left. The elevation of the water surface has dropped only 2 cm in this distance, though y has decreased by 57 cm. The depth is still 12 m at the entrance of the reach, so we have about 4.5 km to go before it gets down to 3.31 m, and will thereafter be parallel to the grade line. The water surface is called a backwater curve. We have calculated only the first section, but it is clear how to proceed. We could, for example, take depths of 11.5, 11.0, 10.5, ... and get to normal depth in about 18 reaches. This is a good job for a computer, which makes calculating water profiles easy and error-free. Why not compute the next step yourself, and find out that this is really not hard at all.

Putting in the dam created a backwater, and it is easy to see why the dam is called a control section. Since we know that the depth will be the critical depth (at least somewhere in the vicinity) we can calculate the critical depth from the discharge Q, and the height of the energy line is determined at that point. Nothing we do to the grade line upstream will make the slightest difference to this. Raising the dam will push the backwater upstream, and lowering it will bring the backwater downstream. Also note that we can find the discharge by simply measuring the height of the water on the spillway. This is the principle of using weirs to measure flow quantity.

If, instead of a dam, we simply made a free outfall at the end of the channel, we would again get critical depth in the vicinity. Because of the curvature of the streamlines at the lip of the outfall, the point of critical depth is moved upstream by 3 to 10 times y_c. The actual depth at the lip is about 0.72 y_c. Now the depths are less than the normal depth, and the depth approaches the normal depth from below as we move upstream, instead of from above, as in a backwater. The water surface is now called a drop-down curve, and can be calculated in exactly the same way as a backwater curve.

The backwater curve and the drop-down curve on a mild slope are the most commonly observed water profiles. The flow is tranquil or upper-stage. The water level rises when the velocity is retarded, and falls when the velocity is increased. If the initial flow is rapid or lower-stage, then the water level is certainly less than the normal level, as well as the critical depth, and the velocity much greater. The velocity must decrease, since it cannot be supported by the mild slope, and the water level must rise. In this case, however, the water does not placidly go through the critical depth, but before this happens a hydraulic jump occurs that makes a turbulent transition to mild flow at a higher level.

Water profiles can be classified by the relative values of the depth, the normal depth and the critical depth, and whether the slope is mild, steep, critical, horizontal or adverse. There are 12 possibilities, of which we have mentioned the 3 occurring on a mild slope, which are by far the most common. There are 3 kinds of water profile on a steep slope, all of which involve a hydraulic jump here or there. There are only 2 kinds of profiles for the special cases of the slope, which do not differ greatly from those on mild or steep slopes. For example, the drop-down curve for a horizontal grade is just like the one for a mild slope. Daugherty gives sketches of the 12 nonuniform flow types (p. 306).

The transition from supercritical to subcritical flow where the profile changes from steep to mild is very different from its inverse. Because the incident flow is more rapid than the wave velocity, information of the coming transition cannot move upstream. In essence, the incident flow collides inelastically with the slowly-moving ahead. Momentum is conserved, but energy is not, and there is usually a significant head loss, and the production of large-scale turbulence. The collision is called a hydraulic jump. A hydraulic jump is characterized by a depth of flow that increases in the downstream direction.

A hydraulic jump is analogous to a shock wave in aerodynamics. It is a turbulent, non-energy-conserving process that passes from rapid flow to tranquil flow. Unlike a shock wave, its front is not vertical, but the depth increases to its final value in a distance about equal to six times the final depth. Since energy is not conserved, the before and after states do not correspond to the intersection of a line E = const. with the specific energy curve. However, momentum is conserved, and this permits us to find the final state if we know the initial state. We will assume the channel is horizontal, since the hydraulic jump takes place in a limited length of channel, and gravitational energies will not be important. Let the water enter the jump with velocity V₁ and height y₁, and leave with velocity V₂ and height y₂. In one second, the momentum lost by the fluid in passing through the jump is ρQ(V₂ - V₁), and this must be equal to the difference in pressure forces on the two cross sections. This difference is ρgh₁A₁ - ρgh₂A₂, where h is the distance from the surface to the centroid of area A. This is one place where the pressure plays an explicit role. Equating the rate of momentum change with the net force acting, we find that the combination hA + QV/g is conserved. For a rectangular channel, A = by and h = y/2m so a conserved quantity is f = q²/yg + y²/2.

We can write this in dimensionless form by setting x = y/y_c, as we did for the specific energy above. Then, f/y_c = 1/x + x²/2. We shall call a plot of f/y_c vs y/y_c the hydraulic jump curve. Curiously, it is just the specific energy curve with 1/x in place of x. The hydraulic jump curve for a wide rectangular channel is shown at the right. The dashed curve is the specific energy curve for the same discharge q. An initial state a is taken into state b by the hydraulic jump. We can combine the hydraulic jump curve with the specific energy curve to find the energy loss in the jump. The connection between the curves is through y/y_c. Horizontal lines through a and b will intersect the specific energy curve at the corresponding energies. It is easy to see that there will always be a decrease in specific energy in the hydraulic jump, since the curves cross at x = 1. Hydraulic jump curves for other channel shapes will be similar.

We can solve the equation f₁ = f₂ to obtain x₂ = (1/2)[-x₁ + √(x₁² + 8/x₁)], relating the heights on the two sides of the hydraulic jump, which are called conjugate depths. The length of the jump is about 6 times the greater height y. If the channel is not horizontal, in the momentum balance we must add the weight of the water between y₁ and y₂ times the sine of the slope, which is S, approximately, since the angle is small.

When the slope changes from steep to mild, a hydraulic jump occurs at a point such that y₂ is the normal depth on the downstream end. Depending on the corresponding value of y₁, the jump may occur either after or before the break in slope, wherever the required value of y₁ can be found. If y₁ is greater than the depth on the steep slope, then the jump will occur on the mild slope when the height of the rapid flow reaches y₁. If it is not, then the jump will occur on the steep slope to a depth that becomes the normal depth on the mild slope.

This may be illustrated by the jump shown in the figure at the left. The water comes through a gate with high velocity and a depth less than the critical depth, so the flow is rapid. The depth conjugate to y₁' is y₂'. Since this is greater than the normal depth on the mild slope, the jump will not occur immediately, because there is insufficient energy. The rapid flow decelerates on the mild slope, and the water depth increases, bringing down the conjugate depth. Both the energy line and the water surface are slightly concave upwards in this region, though drawn as straight. When the depth reaches y₁ conjugate to the normal depth on the mild slope, the jump begins, at the first point where it is possible. It does not occur at a single section, but extends for the length of the turbulent jump (foreshortened in the diagram). It is easy to see that the momentum on the left is balanced by the pressure force on the right. The energy line falls rapidly through the region of the jump, then resumes with the mild slope, S' = S. There is also a small energy loss at the gate, from the level of the slack water upstream. There are other cases, but this is the most common one. A good place to see a jump is at the overflow spillway of a dam, with a rapid flow down the inclined face of the spillway, and a jump on the apron beyond in the tail water.

A hydraulic jump is probably most easily seen if a jet of water issuing from a spout falls normally on a stainless-steel kitchen sink (or in any similar case). Immediately around the point where the jet impacts there is a circular region of smooth flow, then a hydraulic jump when the velocity of the radially diverging water falls below the wave speed. Beyond the jump is a noticeably turbulent flow.

Related to the hydraulic jump is the tidal bore on a river, occurring when the river is shallow, has a funnel-shaped estuary, and the tidal range is large. The jump is not stationary, but moves up the river at a considerable speed, faster than that of surface waves, driven by the pressure of the higher water behind it. The turbulent front may be followed by undulatory disturbances which move with it and are solitons, waves in which nonlinear effects and dispersion combine to create solitary waves. Hydraulic jumps and solitons may often be seen on smooth beaches in wave backwash.

Perhaps the most well-known bores are the equinoctial undulatory bores on the River Severn in western England, easily visible from Sheerness up to the Over bridge near Gloucester. They can be up to 2 m high. The tidal range at Sheerness can be 15 m, and bores occur only when the tide is sufficiently high, at equinoctial spring tides. They were observed by Sir George Airy, the Astronomer Royal, who initiated their theoretical explanation. The largest bore in the world appears to be on the River Qiangtang, which flows past Hangzhou into Hangzhou Wan (Bay). It is up to 9 m high and travels at 25 mph. In this stretch the river is called the Fuchun. The bore on the Amazon is called the pororoca, and can be 4 m high. Several English rivers have bores, known by various names, but the only other prominent one is the eagre on the Trent. There are significant bores on the Brahmaputra and Indus, which flow into the Indian Ocean.

When a bore passes the observer and moves upstream, the direction of the current in the river reverses, and for a while the river flows backwards. At some later time, the flow again reverses and resumes its normal direction.

The famous bore called le mascaret on the Seine has been destroyed by dredging and deepening the river, and the bore on the Petitcodiac off the Bay of Fundy has been similarly mostly eliminated by construction of a causeway. Bores are very sensitive to artificial modifications of the channel. They require rather special conditions to exist, and are not by any means common.

So far we have worked only with rectangular channels to avoid unnecessary complication. Although artificial channels may often be rectangular, other shapes are used, mainly for convenience in construction. The wooden flume is indeed usually rectangular, but circular pipes are easy to obtain in metal and are often used, especially for water supply, sewers, drains and culverts. A canal in earth is usually trapezoidal, to avoid caving of the banks, and concrete channels often imitate this shape. Natural channels we must take as they present themselves.

The most efficient channel will have the minimum wetted perimeter for a given area, or the greatest hydraulic radius for a given area. A rectangular channel of width b and height a has A = ab and P = 2a + b, or R = ab/(2a + b). If A is kept constant, then a db + b da = 0. To find the condition for a minimum P, set dP = 2da + db = (-2a/b)db + db = 0, whence b = 2a, and R = a/2. A semicircular channel of radius r has A = πr²/2 and P = πr, or R = r/2. To be equivalent to the most efficient rectangular channel, 2a² = πr²/2, or r = 2a/√π. Hence R = a/√π = a/1.77, which is greater than the R for the most efficient rectangular channel. The semicircular channel is the most efficient of all. For a circular pipe running full (to which our analysis applies), R = r/2, but now r = √(2/π)a, so R = a/√(2π) = a/2.51. A circular pipe is not more efficient than the most efficient rectangular channel. Remember that there is no friction on a free surface, so a free surface on the boundary of the flow area increases the efficiency.

A simple channel shape that could be used as an example in our analysis is the 90° triangular flume. It is not often found in practice, but is not a bad cross-section at all. If y is the depth from the bottom, A = y² and P = 2√2 y, so that R = y/2√2 = y/2.83. To be equivalent to the most efficient rectangular channel, y = √2 a, or R = a/2. The triangular flume is just as efficient. The specific energy for a triangular flume is E = y + Q²/2gy⁴. Expressing Q as a function of E and y and setting dQ/dy = 0, we find that y_c = (4/5)E. The critical depth is then y_c = (2Q²/g)^1/5. The dimensionless form of E is E/y_c = x + 1/4x⁴. The derivation of the hydraulic jump curve is left to the reader. The centroidal distance of a triangular area is 1/3 of its altitude.

The circular channel running part-full is very commonly met with. The geometry of the channel is shown at the right. The flow occupies a segment of the circle of total angle 2α, related to the depth y as shown. There are tables of the properties of a segment, though the calculations are easy enough on a calculator. In the formulas, α is expressed in radians, but the modifications for using degrees are obvious. Unfortunately, the properties are not suitable for easy algebra, so analytic results are difficult. Solving for normal flow depth in terms of Q and S is not simple. One method would be to tabulate Q as a function of y for the given S, and then find the value of y that corresponds to the given Q. For smooth metal pipes, n = 0.011 to 0.015. For corrugated pipes, the value of n is about twice this. Galvanized corrugated pipes are often used as culverts.

The trapezoidal section is used for canals, especially those excavated in earth, to avoid caving of the banks. The cross-section can be specified by top width t, bottom width b and depth y. The area is A = (t + b)y/2, and the wetted perimeter is P = b + 2√[y² + (t - b)²/4]. By the same method as for the rectangular channel, the most efficient trapezoidal channel is a half-hexagon, with sides of 60° slope. If b is the bottom width, then the top width is 2b, the area A = 3by/2, and the wetted perimeter P = 3b, so the hydraulic radius is y/2. Of course, y = b cos &30° = b√3/2. This section is as bad algebraically as the circular one, since this simple expression for R does not hold when the cross-section is not full.

A canal in earth loses water very readily. This was discovered by many American canal builders in the early days, who thought that making a canal was just a matter of digging a ditch. Their canals rapidly ran out of water, especially when crossing ridge lines. The secret to canals was puddling, or coating the wetted perimeter with an impervious layer of clay tempered with sand that prevented water loss. The sand is to prevent cracking, and good puddle is almost impervious. This, however, requires expensive labor, as does lining with concrete, wood or brick, so most irrigation canals to this day are not puddled or lined, relying on a copious source of water instead. Earth dams, however, often contain puddle in their core wall, that prevents leakage of water through the dam.

A weir (pronounced "we're") is a dam placed across a stream to raise or regulate the water level upstream. The discharge of the stream flows through an opening in the weir, whose lowest level is the sill height. A depth of at least this height is maintained, which becomes a little greater, depending on the actual discharge. The water levels in the River Thames, from Richmond to Oxford, are maintained by numerous weirs, with locks in them to pass river traffic. The Ohio River is also maintained as a slack-water navigation by about 50 dams along its length, which are really weirs. In hydraulic engineering, weirs are used for measuring discharge, for which they are very convenient. Hydraulic weirs are usually thin and sharp-crested, made from sheet metal, because this shape is more amenable to theoretical analysis and reproducibility. Weirs for other purposes usually have broad crests. When we say "weir," we may be referring to the opening for the discharge (as here), or to the whole dam. The word "weir" is from Anglo-Saxon werian, to defend, cognate with the German wehr. We will not give an exhaustive account of hydraulic weirs here, but only explain the principles.

A convenient form of weir for small discharges is the 90° V-notch weir, shown at the left (the drop-down curve is exaggerated). We will assume that the velocity in the approach is negligible, so that the water level is also the energy level, and that the discharge is free, not partially or wholly submerged. We also assume that at the weir, the water depth will be the critical depth y_c. We have already shown that for a triangular channel, Q = √(g/2) yc^5/2. The velocity at the weir is V = Q/y_c², so the velocity head there is y_c/4. Since the specific energy is equal to H (this is the usual symbol for the upstream water depth above the sill), y_c = 4H/5. Expressing the discharge in terms of H, we have Q = √(g/2)(4H/5)^5/2 = 1.267 H^2.5 cms. Using feet instead, we have Q = 2.30 H^2.5 cfs. To find Q, all we have to do is read H from the gauge at the upper end of the drop-down curve and perform a simple calculation.

The two effects we have neglected are the influence of upstream velocity and the contraction at the crest, as in the case of orifices. Upstream velocity can be taken into account by increasing H by the velocity head. We won't make this correction, although it is usually made when precise results are necessary, and will be found in handbooks. Accurate measurments gave Q = 2.52 H^2.47 cfs and 2.48 H^2.48 cfs, the former for commercial sheet metal, the latter for a polished brass plate. The heads varied from 0.2 to 1.8 ft (Q = .05 to 11 cfs, or 0.4 to 82 gal/s). It is clear that our analysis is close to the truth, differing by less than 10% from experimental results. The notch weir is very suitable for laboratory experiments or in a scientific garden.

If we apply the same analysis to a wide rectangular weir, we find that H = 3y_c/2, and the discharge per unit width is q = √g(2/3)^1.5 H^1.5 = 1.70 H^1.5. In feet, q = 3.08 H^1.5. Francis gave the formula q = 3.33 H^1.5, so again our analysis is not far wrong, in spite of its simplicity.

R. L. Daugherty and J. B. Franzini Fluid Mechanics, 6th ed. (New York: McGraw-Hill, 1965). Chapter 10, pp. 276-326.

J. C. Trautwine, The Civil Engineer's Pocket-Book (Philadelphia: Wm. Butter & Co., 1888). pp. 236-281. Kutter's formula, together with much practical information.

L. C. Urquhart, ed., Civil Engineering Handbook, 4th ed. (New York: McGraw-Hill, 1959). Section 4.

H. Lamb, Hydrodynamics, 6th ed. (New York: Dover, 1945).

Thanks to David MacNevin for noticing that I had interchanged supercritical and subcritical, to John Maunsell for an error I made in the specific energy for a triangular channel, and to Daniel Phelps for noticing a missing n!

Composed by J. B. Calvert
Created 19 July 2003
Last revised 6 June 2007