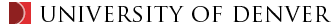1. Introduction

A sliding system such as automotive disk brake or clutch involves two or more sliding bodies in frictional contact. A disturbance might change the otherwise uniform pressure distribution and hence the frictional heat generation. This produces non-uniform thermoelastic distortion and further non-uniformity in the contact pressure distribution. If the sliding speed is sufficiently high, the thermal-mechanical feedback process is unstable, leading eventually to the localization of the load in a small region of the nominal contact area of the sliding surfaces. This phenomenon, generally known as "thermoelastic instability" or TEI, was first discovered and explained by J.R. Barber in sliding systems involving frictional heating (Barber 1969).

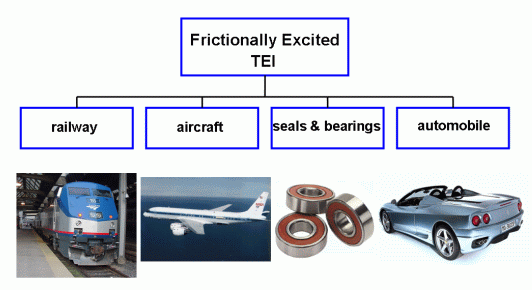
2. HotSpotter

I am the primary author of HotSpotter, a standalone finite element software package for evaluating the susceptibility of disc brakes, clutches or other frictionally sliding systems to thermoelastic instability (TEI). In HotSpotter, An eigenvalue method is used to determine the exponential growth rate of eigenmodes of the system for a given rotational speed. The critical speed is then determined by searching for the lowest speed at which at least one mode has a positive growth rate. There are two sister versions of the code: "classic" and "full3D". The "classic" version is appropriate for clutch problems. In this version linear perturbations on the constant speed solution are sought that vary sinusoidally in the circumferential direction and grow exponentially in time. These factors cancel in the governing thermoelastic and heat conduction equations, leading to an eigenvalue problem on the two-dimensional cross-sectional domain for the exponential growth rate for each Fourier wave number. (Yi et al. 2000) The Fourier reduction method developed in HotSpotter permits a remarkably efficient solution of the frictional thermoelastic stability problem for systems in which the geometry is axisymmetric. The "full3D" version is appropriate for disc brakes where the geometry is not axisymmetric. In this version the model has to be constructed using 3D elements and some finite element skills are needed by the user. User input to the software includes the geometric shape of all the components, the relevant material properties, the coefficient of friction and the boundary conditions. Output from the program includes the exponential growth rates of the eigenmodes, the critical speed as a function of hot spot number and the spatial forms of the dominant eigenmodes.

HotSpotter was originally developed on the Matlab platform and the source code was later compiled into a C program using the Matlab C-compiler. The trial version of HotSpotter for Windows can be downloaded from the link below. Both the "classic" and "full3D" versions have been integrated into a single package. A User's Manual is also available and included in the file. After you complete downloading, please follow the steps below to run HotSpotter.

Step 1: Click "MCRInstaller_Win64.exe" to install the Matlab runtime components.

Step 2: Click "hotspotter_Win64.exe" to run HotSpotter.

Please note that most of the modules in this trial version of HotSpotter are fully functional and the simulation results of some sample models are also viewable. However, users are unable to perform any new analysis. Please contact Professor J.R. Barber or University of Michigan Tech Transfer Office if you are interested in purchasing the full version of HotSpotter. Once the license fee is paid, I will send you a registration file with which the analysis module in the code will be unlocked so that you can perform an analysis on your own model.

Click either of the following two links to download the latest version of Hotspotter (Win64):

download link A (Univ of Denver server)

download link B (Google Drive)

Earlier versions are also available at the following sites:

download link C (MSN One Drive)

download link D (Baidu Drive)

If your computer uses the old 32-bit Windows system, click the following link to download Hotspotter (Win32):

download link E (Baidu Drive)



References

Barber, J.R., 1969, Thermoelastic instabilities in the sliding of conforming solids, Proc. R. Soc. Lond. A312, 381-394.

Yi, Y. B., Barber, J. R., and Zagrodzki, P., 2000, Eigenvalue solution of thermoelastic instability problems using Fourier reduction, Proc. Roy. Soc. London , A456, 2799-2821.