Research areas
Light’s orbital angular momentum
A new twist on light
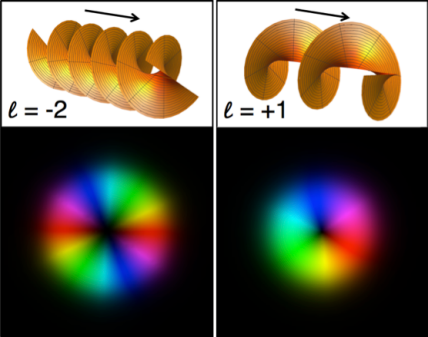
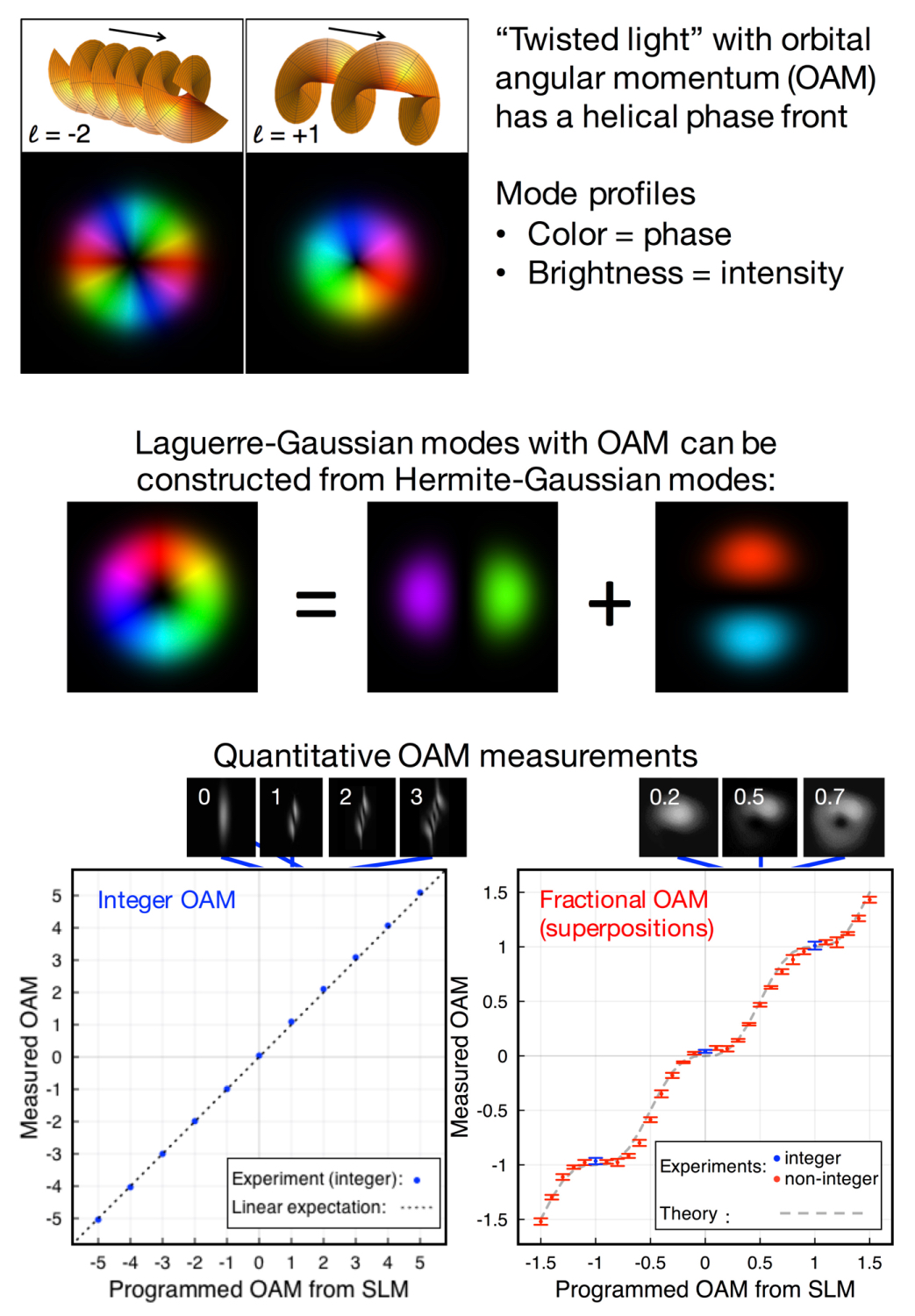
It has long been understood that light carries linear momentum (p = ℏk) related to its wavelength and spin angular momentum (SAM = ±ℏ) related to its polarization. However, it wasn’t until the early 1990’s when scientists realized that laser beams with an azimuthal (around-the-beam) phase wrap carry additional “orbital" angular momentum (OAM = 𝓁ℏ, where 𝓁 is an integer “winding number” indicating the number of times the phase wraps azimuthally around a beam). This OAM has the appealing properties of being discrete but being a potentially unmilited basis.
This discovery of “twisted light” with orbital angular momentum (OAM) has generated a lot of excitement because of the potential applications, especially for using the discrete OAM basis to increase bandwidth for communications. Additionally, the orbital angular momentum carried by twisted light can be used to spin micromachines and interact with rotating objects.
We are interested in fundamental questions related to the generation, propagation, and measurement of twisted light with OAM, such as:
How does mixing OAM modes affect topology, specifically vortex splitting?
How can light's OAM be generated and quantitatively measured inexpensiveily and flexibly?
How do simple optical interactions with interfaces, such as reflection, refraction, and diffraction, affect light’s OAM?
Coherent spectroscopy of nanostructures
Carrier dynamics in new spectral dimensions
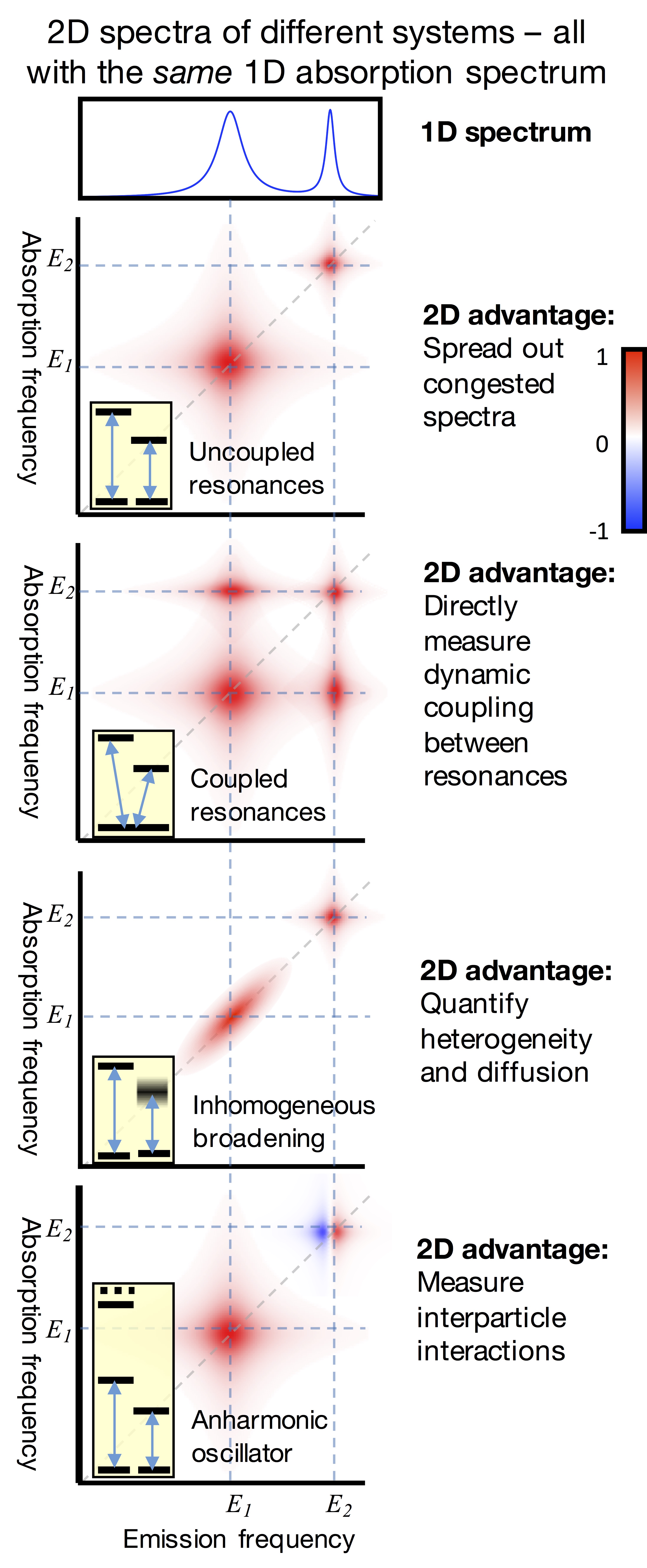
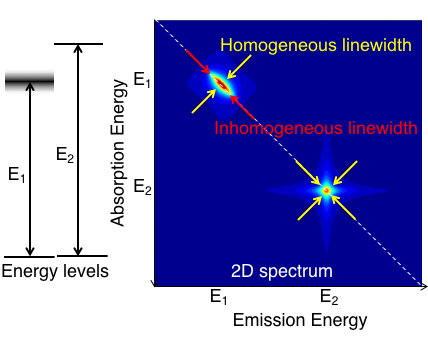
Experimental measurements of optical nanostructure resonances are complicated by numerous (often overlapping) interactions and decay channels. Two-dimensional coherent spectroscopy (2DCS) unfolds resonance information over two dimensions typically corresponding to absorption and emission frequencies, isolating couplings and allowing for quantitative measurement. 2DCS has been applied successfully and extensively using infrared light to observe vibrational excitations in molecules and liquids, but it has only recently been extended to the optical regime. 2DC spectra have many advantages over one-dimensional analogs. Coherent interaction pathways can be isolated and clearly defined when spread over two spectral dimensions and resonances corresponding to intra-action and interactions between quantum states can be differentiated, making 2DCS a powerful tool for studying energy transport between and within confined nanostructures. Also, the homogeneous and inhomogeneous contributions to resonance linewidths can be separated and measured independently. That is, information about an ensemble of individual resonances (each corresponding to a quantum dot of a particular size) can be recorded in a single measurement, and the dynamics of a particular resonance can be extracted analytically from the 2D spectrum. This allows us to study an entire ensemble of nanostructures with widely-varying sizes and recover the homogeneous dynamics of each nanostructure, rather than resorting to multiple studies of single-structure properties.
We are using our 2DCS system to pursue many basic questions about electron dynamics in nanostructures, such as:
What does a 2D spectrum tell us about inter-particle interactions? How does this change in nanostructures that are so small that electron wavefunctions are confined?
What quantum pathways are active in nanomaterials with different unique properties, such as high photoconversion efficiency?
How can we further enhance the spectral resolution?
How does twisted light with orbital angular momentum (OAM, see section above) affect optical transitions in semiconductor nanostructures?